3.9 Photogrammetrischer Ansatz
Die Photogrammetrie ist eine eigenständige Methodik der Geofernerkundung und nutzt die mathematisch-geometrischen Information von Photographien (Photo - Grammetrie = Bild-Messung) zur genauen Erfassung der Topographie und quantifizierbarer Topologien. Für die Geowisssenschaften ist besonders die Aerophotogrammetrie wichtig - derartige Aufnahmen können genähert als Senkrechtaufnahme gelten. Ihr gegenüber steht die terrestrische Photogrammetrie. Sie analysiert terrestrische Bilder unter gleichbleibenden Aufnahmebedingungen (z.B. Orientierungsparameter teilweise direkt messbar, z.B. bzgl. Hausfassaden), aber die Aufnahmegeometrie ist in der Regel weit von der "idealen" Senkrechtaufnahme entfernt!
Wenn hochauflösende Fernerkundungsdaten, vor allem Luftbilder von Drohnen (UAV) oder Flugzeugen, verfügbar sind, besitzen diese Verfahren ein hohes Potential, an der Erdoberfläche sichtbare Erscheinungen dreidimensional zu interpretieren und ihre absolute Geometrie zu bestimmen. Sensoren der Photogrammetrie sind analoge und digitale photographische Systeme aber auch multispektrale Scanner.
Die Leistungsmerkmale der Photogrammetrie sind:
- berührungslos (remote sensing)
- flexibler Aufnahmezeitpunkt
- Speicherung aller für den Sensor "sichtbaren" Oberflächeninformation bis hin zum Auflösungsvermögen des Sensors (ca. 30-40 Linien/mm bei photographischem Film, d.h. wenige mm/pixel)
- sehr effektive und geometrisch stabile Speicherung
- Information jederzeit extrahierbar und vielfältig analysierbar
- flächenhafte Information und mathematische Analyse.
Die Nachteile der Photogrammetrie sind :
- nur Oberflächendaten (Tiefeninformation zusammen mit z.B. Geophysik und Modellen)
- keine Wolkendurchdringung
- Probleme durch Beleuchtung, Schatten, fehlende Kontraste
- Hoher Korrekturaufwand (Kamerakalibrierung, Verzerrungen, Zentralperspektive, u.a.)
- hohe zeitliche Auflösung bei Luftbildern nur sehr aufwendig möglich
- hoher Bildflug- und Auswerteaufwand
Bei digitalen Luftbildkammern kommen neben der aufwendigen Kalibrierung der Kamera, die notwendigen großen Speicherkapazitäten an Bord der Sensorplatform (Flugzeug) und des 'back up' (Datensicherung) hinzu.
Mathematische Grundlagen oben
Für die Senkrechtaufnahme gilt (a):
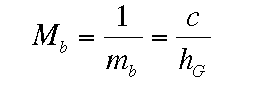
Mb: Bildmaßstab
mb: Massstabszahl
c: Kammerkonstante (kalibrierte Brennweite)
hG: Flughöhe über Grund
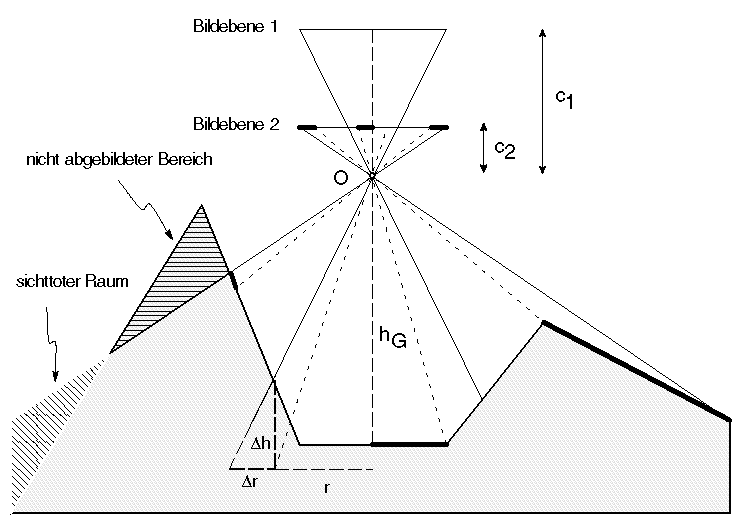
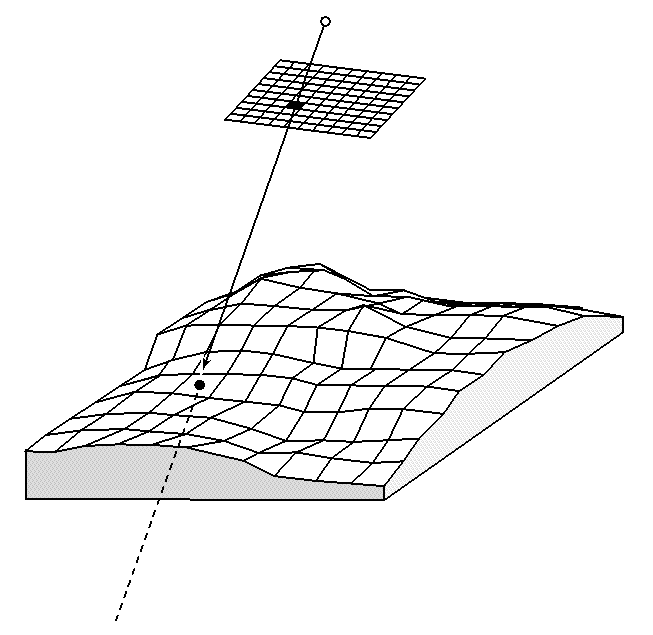
Gleichung (a) gilt streng nur bei horizontalem, ebenen Gelände. Höhenunterschiede im Gelände verändern die Flughöhe über Grund und damit den Maßstab im entsprechenden Bildpunkt. Daher wird besonders im bewegten Gelände ein Maßstabsbereich (z.B. 1: 21.000-1: 25.000) oder ein mittlerer Maßstab (bezogen auf die mittlere Geländehöhe oder den Geländeauschnitt von besonderem Interesse) angegeben (Abb.3.9.1).
|
Abb. 3.9.1.: Senkrecht- |
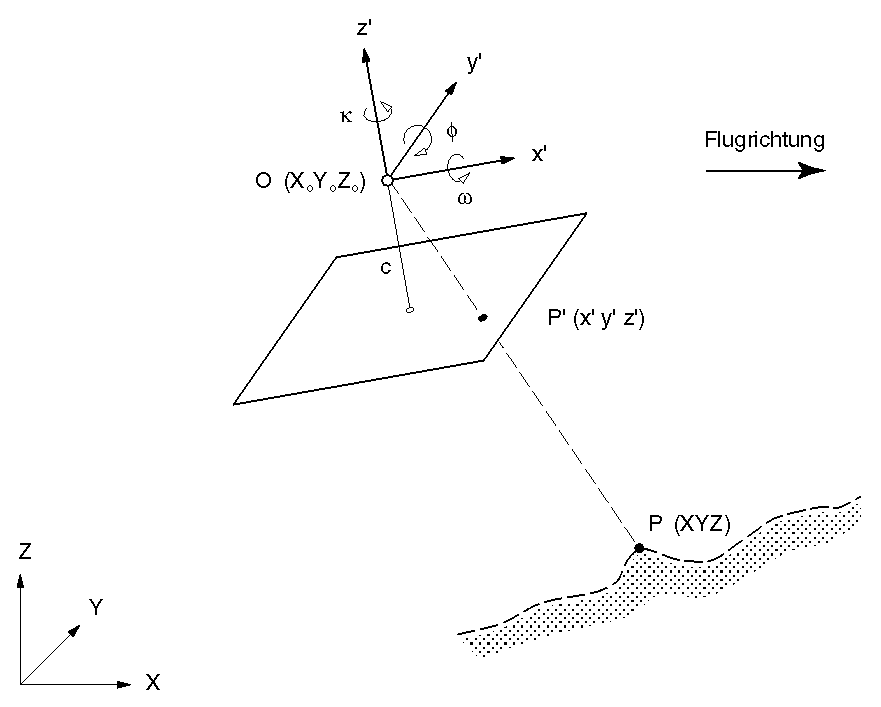
Für die Schrägaufnahme gilt die allg. Grundformel der Photogrammetrie (b) :
|
Abb. 3.9.2: Zusammenhang hinsichtlich der Zentralprojektion des Geländes in die Bildebene des photo-graphischen Sensors. Einzelbild-auswertung (Uni-Zürich, 2003). |
Der Bildverband oben
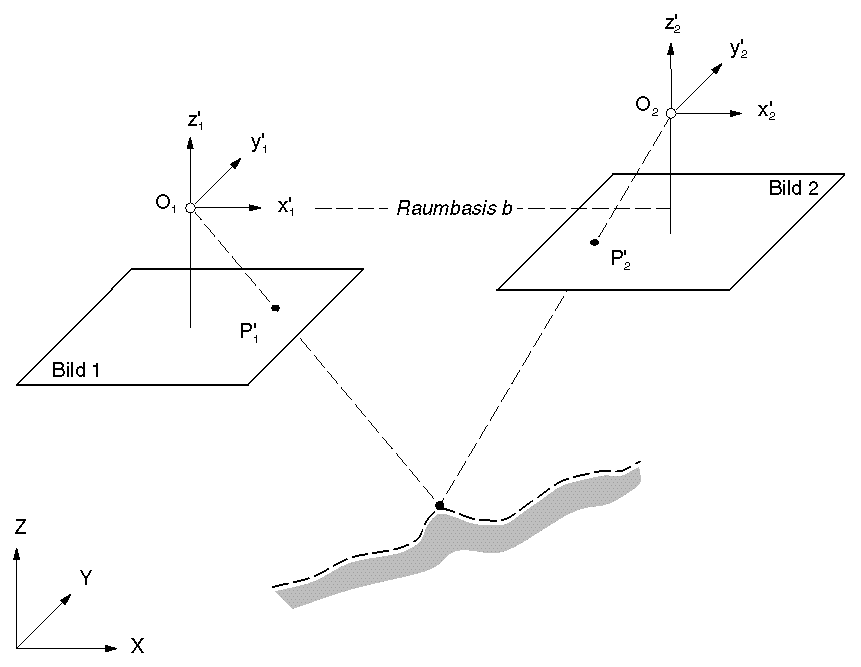
Bei Reihenbefliegungen und Überlappung von 60% (bei Drohnen häufig 80%) sind auf mehreren Bildern ist derselbe Geländepunkt abgebildet (gemeinsame Tie-Points in zwei Bildern unter Paralaxenbildung: Stereoeindruck!). Durch das Projektionszentrum O und einen Bildpunkt wird eine Raumgerade aufgespannt. Werden in mehreren Bildern identische Bildpunkte gewählt bzw. deren Bildkoordinaten gemessen, kann ein unbekannter Geländepunkt bei bekannter Orientierung der Bilder durch 3-dimensionalen Geradenschnitt bestimmt werden. Die beiden Projektionszentren und der Bildpunkt, bzw. die beiden "Kernstrahlen" spannen eine "Kernebene" auf (c).
![]()
|
Abb. 3.9.3: Geometrie in einem photo-grammetrischen Stereomodell. Punktbestimmung durch Geradenschnitt (Uni-Zürich, 2003). |
Die Bildorientierung oben
Die Bildorientierung umfasst alle Parameter die nötig sind um den Bezug zwischen dem Gelände/Objekt und seiner Abbildung herzustellen. Dies sind insbesondere
-
Parameter der inneren Orientierung:
Lage des Bildhauptpunktes bezüglich des Projektionszentrums, d.h. unter anderem Kammerkonstante c (vgl. Gleichung (b)). Definition bezüglich der Rahmenmarken -> Rahmenmarken legen das Bildkoordinatensystem fest. Ein analoges Messbild enthält mindestens vier Rahmenmarken, an jeder Seite des Bildes bzw. in den Ecken je eine. Der Ursprung der Bildkoordinaten ist in Bezug auf den Schnitt der Verbindungsgeraden der Rahmenmarken kalibriert. Die Rahmenmarken werden bei jeder Aufnahme auf das Messbild projiziert. Die Lage der Rahmenmarken ist kalibriert (Kalibrierungsprotokoll). Durch kalibrierte Rahmenmarken kann ausserdem ein möglicher Filmverzug festgestellt und berücksichtigt werden. Digitale Aufnahmen besitzen keine Rahmenmarken, d.h. die Dimensionen der verbauten CCD-Zelle definieren direkt das resultierende Bildkoordinatensystem!
- Parameter der äusseren Orientierung:
räumliche Drehmatrix (3 unbekannte Drehwinkel), Koordinaten des Projektionszentrums im System der Geländekoordinaten (3 unbekannte Translationen), Maßstab
- Bestimmung durch Passpunkte, deren Geländekoordinaten bekannt sind. Durch Verwendung mehrer Passpunkte und Aufstellen eines entsprechenden Gleichungssystemes aus je einer Gleichung pro Passpunkt können die Paramter der äusseren Orientierung bestimmt werden .
-Im Bildverband kann die äussere Orientierung in relative Orientierung (Orientierung der Bilder zueinander, aber ohne Geländebezug) und absolute Orientierung (Geländebezug des Bildverbandes) unterteilt werden.
Das Ein-, Zwei- und Mehrbildverfahren oben
Einbildverfahren
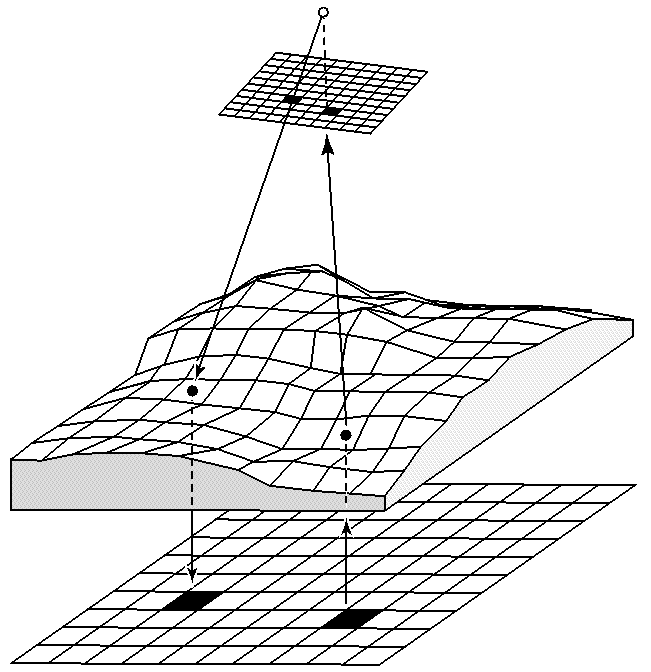
- Orthoprojektion (OP): Bei bekannter Geländehöhe (z.B digitales Höhenmodell DHM) und bekannter Bildorientierung können für jeden Bildpixel die Lagekoordinaten im Geländesystem berechnet werden. Damit kann das Bild in eine definierte Projektion transformiert werden (zumeist Orthogonalprojektion, aber z.B. auch Perspektiven). Es erfolgt eine flächenhafte (bildweise) Bildverarbeitung (Abb. 3.9.4).
Probleme: Durch Verdeckung/Schatten im Originalbild kann es zu fehlender Bildinformation kommen. Als Folge werden Lücken einfach 'aufgefüllt'. Höhenfehler im zugrundeliegenden DHM führen zu Lagefehlern im OP (vergleiche dh und dr in Abb. 3.9.2; z.B. verkippte Häuser, Brücken oder Bäume, die im DHM nicht enthalten sind). Anwendung: Aufdeckung von DHM-Fehlern durch Vergleich zweier OP, die aus verschiedenen Bildern, aber demselben DHM erstellt wurden, denn DHM-Fehler führen zu unterschiedlichen Lagefehlern in beiden OP!
Im Orthophoto sind dann direkt Messungen (xyz) möglich (Abb. 3.9.5) . Eine Überlagerung ist mit anderer, vor allem vektorieller Information möglich. Zugleich Erhaltung des hohen Informationsgehaltes eines Bildes. Die Integration des OP ist als Datenebene in ein GIS nun erst möglich! Digitalisierung am Bildschirm direkt in Geländekoordinaten (orthogonaler Raumbezug!).
|
Abb. 3.9.4 : Orthoprojektion in zwei Varianten: Punkt A (links) Wählen eines Bildpixels, Berechnung der Lagekoordinaten im Geländesystem mit Hilfe der Höhe des Punktes (interpoliert aus DHM, entspricht Monoplotting), Abbildung des Pixels in Orthogonal-projektion. Punkt B (rechts) Wahl eines (noch leeren ) Pixels im Orthophoto (Lagekoordinaten im Geländesystem), Interpolation der entsprechenden Geländehöhe aus DHM, Berechnung der zugehörigen Bildkoordinaten, Grauwert- (bzw. Farb-) Interpolation im Bild und Abbildung dieser Werte im Orthophoto (Uni-Zürich, 2003). |
|
Abb. 3.9.5: Monoplotting. Wahl eines Bildpunktes und Berechnung der 3D-Koordinaten im Geländesystem durch Geradenschnitt mit dem DHM (Uni-Zürich, 2003). |
- Monoplotting: Bei bekannter Geländehöhe (DHM) und bekannter Bildorientierung können aus den Bildkoordinaten eines Punktes seine 3D-Koordinaten im Geländesystem berechnet werden (punktweise Bildauswertung).
Zweibild- (Stereo-) verfahren oben
- Punktbestimmung: Bestimmung der 3D-Geländekoordinaten von Geländepunkten durch Messung der Bildkoordinaten desselben Punktes (identisch, korrespondierend) in beiden Bildern (vgl. Abb. 3.9.3). Diese Messung kann theoretisch sequentiell oder gleichzeitig (simultan) in beiden Bilder erfolgen. In der Praxis geschieht die Messung in der Regel simultan unter Ausnutzung des Stereoeindruckes. Weiter wird in entsprechenden Auswertegeräten berücksichtigt, dass der gesuchte Punkt und die beiden Projektionszentren eine Ebene aufspannen (Kernebene). Diese geometrische Zusatzbedingung reduziert bei der Auswertung die Freiheitsgrade bei der Suche der korrespondierenden Punkte. Bei Messung von Einzelpunkten werden die Koordinaten punktweise abgespeichert. Durch Abfahren einer Linie (z.B. Grundrisslinie, Höhenlinie, Höhenprofile) und kontinuierliche (inkrementelle) Aufzeichnung der Koordinaten kann (quasi) linienweise ausgewertet werden.
- Grundriss- / Lageauswertung: Bestimmung der ebenen Geländekoordinaten (2D, X und Y) von Punkten und Linien, von denen nur deren Lage interessiert (Seeränder, Wege/Strassen/Häuser für Lagekartierungen, Umrisse etc.). Genauigkeit in der Praxis mit hochpräzisen Auswertegeräten bis ca. 10-40 µm.
Vorsicht: Definitionsunsicherheit im Gelände!
- Höhenauswertung: Bestimmung von 3D-Geländekoordinaten von Einzelpunkten, Linien, Höhenlinien, Höhenprofilen, Punktrastern, Bruchkanten und anderen (z.B morphologisch bedeutsamen) Punkten und Linien -> z.B. Erstellung eines DTM! Genauigkeit bis zu ca. 0.02% der Flughöhe über Grund (hG; vgl. Abb. und Formeln oben!). Unter Umständen sind die Lagekoordinaten der zu bestimmenden Punkte bereits definiert, und dann nur noch jeweils die Höhen zu messen (z.B. regelmässiges Raster-DTM, Höhenprofil).
- Wiederholung obiger Auswertungen: Multitemporale Auswertungen. Veränderungen im Grundriss (z.B. Infrastruktur, Flüsse, Waldbrände, Lava, Gletscher, Vegetation etc.) und in der Höhe (z.B. Massenverschiebungen).
Mehrbildverfahren oben
Verknüpfung eines Bildverbandes über identische Bildpunkte -> gemeinsame Orientierung. Aerotriangulation: Keine Orientierungsübertragung bekannter Geländepasspunkte für jedes Einzelbild, sondern (automatisiert) über den ganzen Bildblock verteilt. Bestimmung der Orientierungsparameter, der Pass- und anderer Punkte im Zuge einer gemeinsamen Ausgleichung (Bündelblockausgleichung).
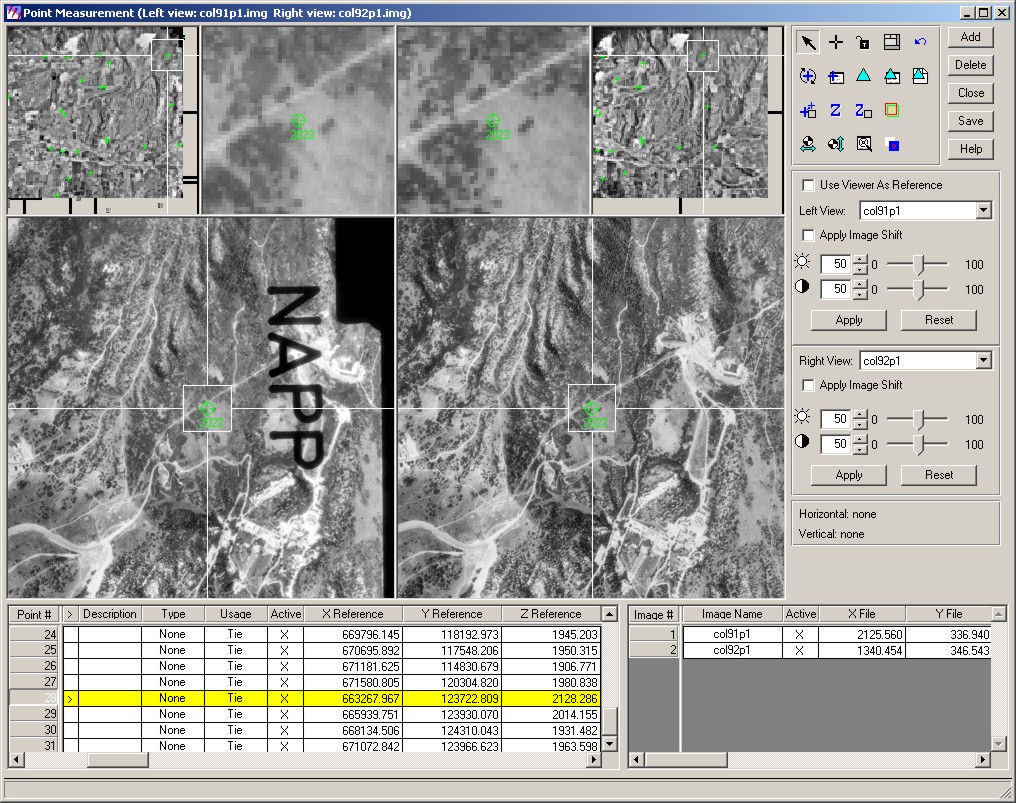
Punktbestimmung einzelner Punkte nicht nur aus zwei, sondern mit mehreren Bildern -> Schnitt von mehr als zwei Geraden = überbestimmter Geradenschnitt. Nur rein rechnerisch möglich (digitale Photogrammetrie), da Betrachter nur in maximal zwei Bilder simultan messen kann.
|
Abb.3.9.6: Beispiel einer Punkt- |
Auswertegeräte oben
Analytische Auswerteverfahren (UAV/UAS)
Computergestützte Messung von Verknüpfungspunkten/Bildkoordinaten und 3D Auswertung durch Software wie Pix4D, Agisoft, Drone2Map oder vergleichbare Open Source Produkte (z.B. OpenDroneMap/ODM). Die Berechnungen folgen prinzipiell den Gleichungen b) und c).
Der Arbeitsablauf gliedert sich in die grundsätzlichen Schritte
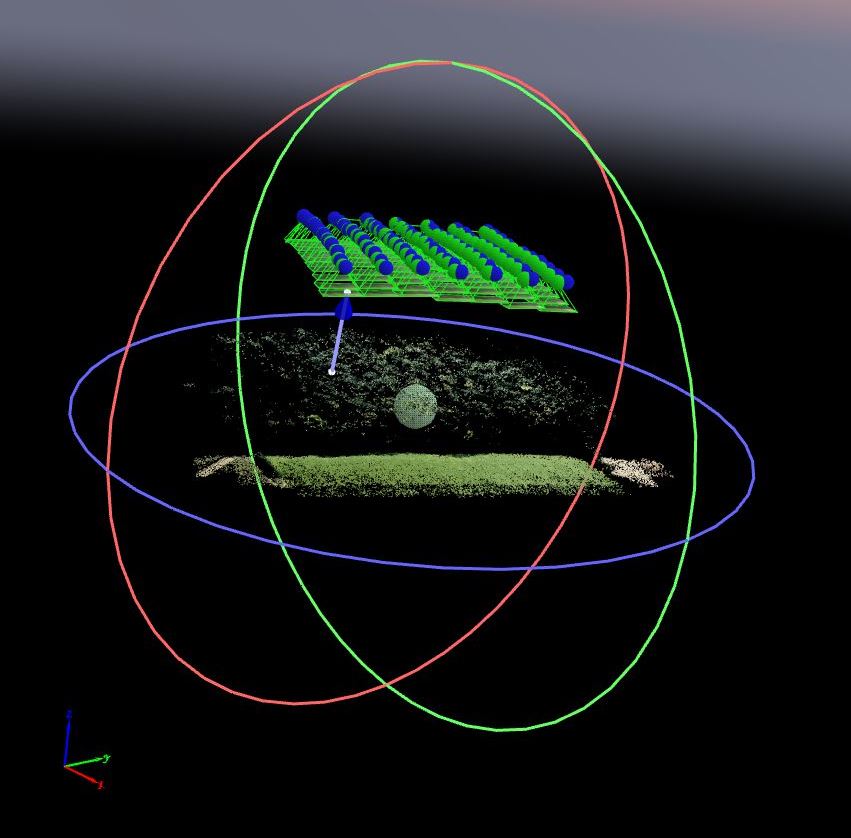
- Einzelbilder zu Mosaik zusammenfügen (mittels Image-GeoTags, GPS-Punkte und/oder Bildverknüpfung/Tiepoints)
|
Abb.3.9.7: Beispiel einer 3D Punktwolke, Orthomosaik und Bildverband aus UAV-Daten mittels Pix4D. |
Digitale Photogrammetrische Einzelbildsysteme oben
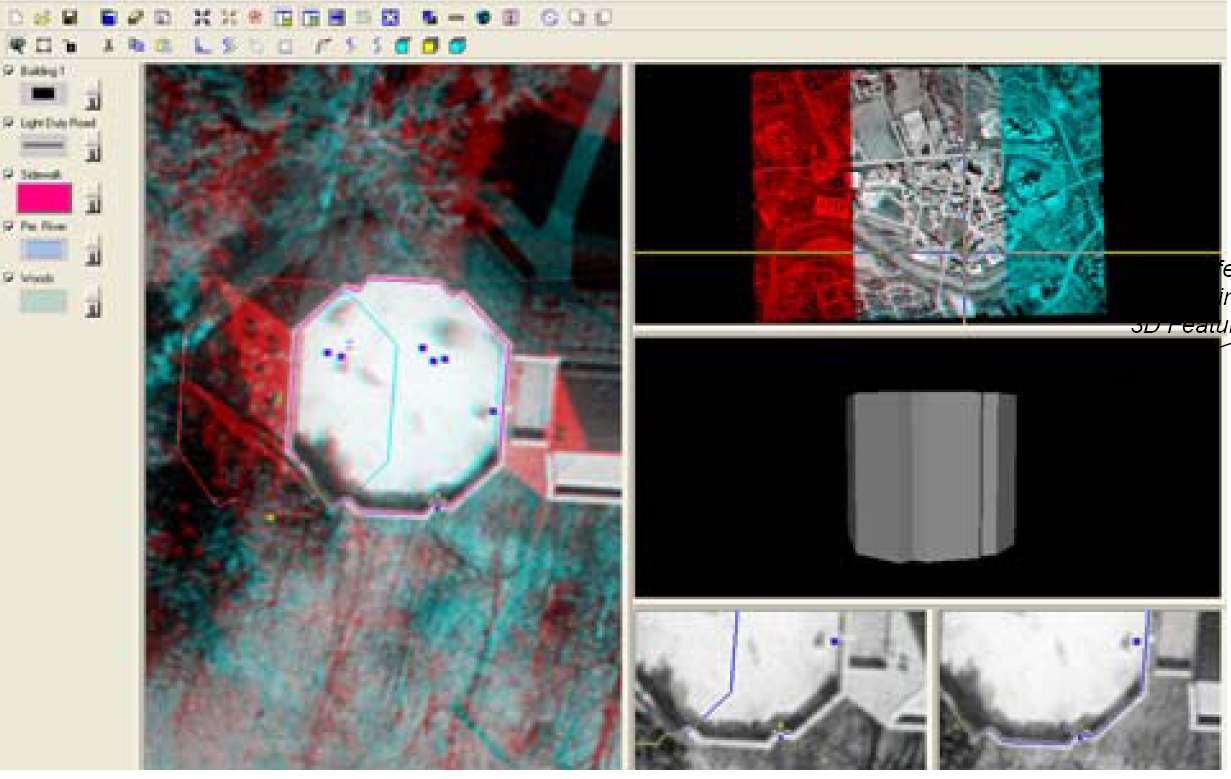
Digitale Photogrammetrie mit Monosystemen (normale, leistungsfähige Hardware, aber spezielle Software) ist auch möglich. Z.B. digitale Orthoprojektion oder Monoplotting. Bei Stereosystemen spielt vor allem die Stereobetrachtung am Bildschirm eine große Rolle. Hier werden den Augen getrennte Bilder zugeführt. Dies erfolgt durch Stereoskope, Anaglyphen (Farbtrennung), polarisiertes Licht oder Shutter-Brillen. Neue Entwicklung wie z.B. autostereoskopische LC Displays (paralleles Licht) erlauben mittels des entstehenden Steroeffektes in Ortholuftbildpaaren 3D-Formen (Features) zu extrahieren, so z.B. Gebäude, Landschaftselemente oder Reliefformen (Abb. 3.9.9).
|
Abb. 3.9.8: Digitale photogrammetrische Station mit Scanner und Stereobetrachtung durch Linsensystem (Stereoskop). Weitere Gerätebeispiele: Leica, Zeiss ca. 2005. |
|
Abb. 3.9.9: Digitale Extraktion von 3D-Elementen unter LPS (ERDAS) aus Ortho-Anaglyphenbildern. |
Zusammenfassende Charakteristika der digitaler Photogrammetrie:
Vorteile
- keine speziellen, hochpräzisen mechanischen Geräte im Feld
- geometrisch genauere Vermessung als durch SfM-Strategien (vgl. auch Kap. 3.8)
- geometrisch absolut stabile Lagerung (durch Speicherung der digitalen Bilder)
- Kombination von manueller, halbautomatischer und automatischer Messung/Bildverarbeitung/Bildanalyse
- Kombination verschiedener Sensoren möglich
- Datengewinnung, -Verarbeitung, -Editierung, -Speicherung und -Verwaltung in einem System
- Mehrbildverarbeitung/Blockbildung mit vielen Aufnahmen möglich (vgl. Abb. 3.9.6)
- Finden und Messen identischer Punkte in mehreren Bildern durch automatische digitale Grauwertkorrelation (-> z.B. automatische DHM-Messung)
Nachteile
- komplexe Prozessketten/Kontrollaufwand
- Auflösung derzeitiger CCD-arrays geringer als menschliches Auge: 30µm vs. 70µm (Vergrösserungen aber möglich!)
- Auflösung Bildschirm 200-300µm
- Speicherbedarf eines digitalen (auch gescannten) Luftbildes liegt schnell im GByte-Bereich/Bild, bei mehreren hundert bis tausend Bildern im Verband/pro Mission!