2.3 Geometrie der Bilder

Zwischen den mit Fernerkundungssystemen gewonnen Bilddaten und der Geländeoberfläche bestehen in Abhängigkeit des jeweiligen FE-Sensors strenge geometrische Beziehungen. Die Photogrammetrie macht sich diese Beziehungen zu Nutze um Messungen innerhalb der aufgenommenen Flächen vorzunehmen und so genau wie möglich in Karten zu überführen. Photogrammetrische Anwendungen sind mittlerweile so komplex geworden, daß hier eine eigenständige Disziplin der Vermessungstechnik entstanden ist.

Aber auch thematisch arbeitende Bildauswertung muß eine angemessene Genauigkeit in ihren Karten erreichen und sehr genaue geometrische Korrektur der Daten vornehmen. Diese Korrekturen erfolgen vor der Interpretation, damit die thematischen Ergebnisse direkt in ein gültiges Raumbezugssystem (z.B.UTM, WGS 84 oder Gauss Krüger) übertragen werden können.

Geometrische Eigenschaften von Photos, Scanner- und SAR-Daten
In der Geofernerkundung treten erfahrungsgemäß drei Gruppen von Sensoren mit ihren spezifischen geometrischen Abbildungscharakteristika in den Vordergrund: Photographische Systeme, Scanner-Systeme und Radar-Systeme. Bei all diesen Systemen wirken sich Höhenunterschiede und Projektionsart ganz unterschiedlich auf die Bildgeometrie aus (Abb. 2.3.1).

- Photographische Systeme bilden die Erdoberfläche in Zentralperspektive ab! Höher gelegene Geländepunkte, d.h. Punkte oberhalb einer zu wählenden Bezugshöhe, werden dabei in Senkrechtbildern von der Bildmitte radial nach außen versetzt (und umgekehrt!) wiedergegeben (Radialverzerrung).

- Scanner-Systeme ergeben - ideale Flugbahnen vorrausgesetzt - eine Mischprojektion aus paralleler (in Flugrichtung) und zentraler Projektion (senkrecht zur Ebene). Demnach werden höher gelegene Punkte (im Gegensatz zur Photographie) nur senkrecht zur Flugrichtung nach Außen versetzt.

- Radar-Systeme weisen ebenfalls eine gemischte Projektion auf: In der Flugrichtung liegt eine (je nach Neigungswinkel) eingeschränkte Parallelprojektion vor; senkrecht zur Bildebene eine Schrägentfernungsprojektion in der höher gelegene Geländepunkte, die ja von der ausgesandten Wellenfront zuerst getroffen werden, zum Flugweg hin versetzt erscheinen.

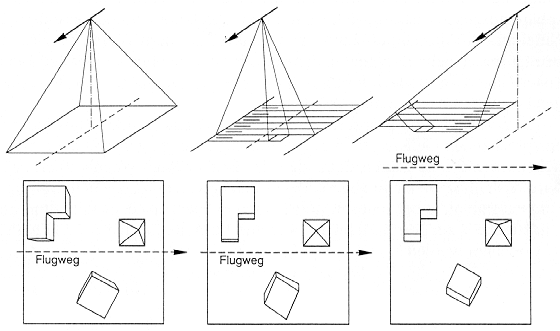Abb. 2.3.1: Schematisierte Abbildungsgeometrie von Photo-, Scanner- und Radar-Systemen (aus Albertz, 1991)

Photographische Bilder oben
Die geometrischen Eigenschaften der (digitalen) photographischen Aufnahme stehen im Mittelpunkt der (digitalen) Photogrammetrie und sollen deshalb an dieser Stelle nicht zu ausführlich behandelt werden (siehe auch Konecny & Lehmann, 1984; Kraus, 1982 und Rüger et al., 1987). Grundlagen der Luftbildinterpretation sind bei Weimann (1984) beschrieben - die wichtigsten Sachverhalte können jedoch zusammenfassend wie folgt dargestellt werden:

Nach Art der Aufnahmen unterscheidet man bei photographisch gewonnenen Bilddaten (z.T. auch bei Satelliten!) zwei Typen, nämlich die Schrägaufnahme (oblique photography) und die Senkrechtaufnahme (nadir-point photography) . Die Schrägaufnahme weist einen deutlichen Winkel zwischen Erdoberfläche und Projektionsebene auf. Sie dient meist allgemeineren Übersichtszwecken und der Erzeugung von Oberflächenpunktwolken für 3D Modelle, insbesondere in der UAS-Fernerkundung - sie soll hier nicht weiter vertiefend behandelt werden.

Die Senkrechtaufnahme ist hingegen von Bedeutung für die klassische Geofernerkundung, da mit ihr systematisch große Areale photographisch zu Kartierzwecken (Mosaiken) aufgenommen werden. Hier ist besonders die Auswertung von Stereo-Luftbildpaaren sowie die Ableitung von Orthophotos, Höhenmodellen und anderer 3D-Daten zu erwähnen.

Die im Bild wiedergegebene Fläche ist etwa quadratisch begrenzt und der Bildmaßstab für alle Bilder gleicher Flughöhe und Kamerabrennweite identisch. Die Aufnahme erfolgt in festgelegten Flugmustern (Befliegungsplänen) mit Überlappung von ca. 60% in Flugrichtung sowie ca. 20% in Seitenrichtung, damit kontinuierliche Flugbahnen mit Stereoaufnahmen abgedeckt werden können (Abb. 2.3.2).

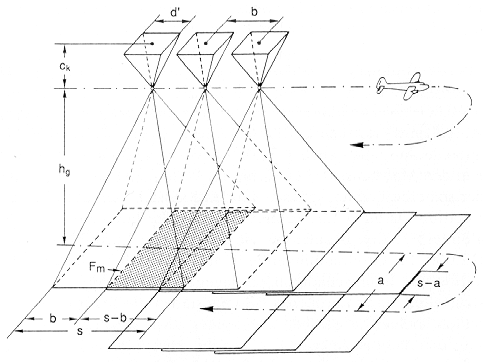Abb. 2.3.2: Schematisierte Flugbahn von flugzeuggetragenen Kameras (aus Albertz, 1991)

Die ideale lotrechte Aufnahme ist im Normalfall meist nicht möglich, da das Flugzeug turbulenten Schwankungen während des Fluges ausgesetzt ist. Dennoch sind die Abweichungen vom Lot i.d.R. sehr gering, so daß man von Senkrechtaufnahmen im weiteren Sinne sprechen kann. Als Bildmaßstab Mb bezeichnet man das Verhältnis einer Bildstrecke zur entsprechenden Geländestrecke. Die Aufnahmeneigung und die Geländehöhenunterschiede führen genau genommen zu einem uneinheitlichen Bildmaßstab; dieser wird allerdings als abgerunderter Zahlenwert angegeben.

Sofern der Maßstab nicht bekannt sein sollte, kann man ihn leicht aus dem Verhältnis einer Bildstrecke s' zu einer Kartenstrecke s oder von Kammerkonstante c zu Flughöhe hg errechnen:

Mb = 1 : mb = s' : s = ck : hg

In einer topographischen Karte ist das Gelände senkrecht auf eine horizontale Bezugsfläche projiziert (Parallelprojektion!). Im Gegensatz dazu stellt das Luftbild eine Zentralprojektion (Abb. 2.3.3) dar. Dies hat zur Folge, daß Objektpunkte, welche über der Bezugsfläche liegen, vom Bildnadirpunkt (Mittelpunkt) radial nach außen versetzt werden; darunter liegende nach innen! Vertikale Objekte (z.B. Bäume) konvergieren deshalb stets zur Bildmitte hin! Dieser Effekt ist umso stärker, je größer der Achsenwinkel vom Nadirpunkt ist (also nach Aussen verlegt ist); in der Bildmitte verschwindet er ganz.

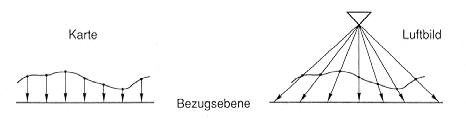Abb. 2.3.3: Schematisierte Projektionen des Geländes in Karte und Luftbild (aus Albertz, 1991)

Die Kenntnis dieser Zusammenhänge kann dazu dienen, auf einfache Weise die Höhe der Objekte zu bestimmen. Wenn der Objekthochpunkt und der darunter befindliche Fußpunkt eines Objektes zu sehen ist, kann man aus der radialen Versetzung der Punkte (r') die Objekthöhe (h) ableiten (Abb. 2.3.4):

Dh = ( Dr' : r') hg

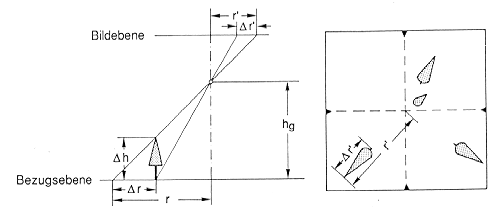Abb. 2.3.4: Schematisierte radiale Versetzung durch Höhenunterschiede (aus Albertz, 1991)

Ebenso ist es möglich die Objekthöhe aus der Schattenlänge l zu ermitteln, wenn der Schlagschatten auf eine horizontale Fläche fällt und die Sonnenhöhe a (Winkel!) über dem Horizont bekannt ist. Sofern mindestens eine Objekthöhe bekannt ist, genügt auch das Verhältnis der Schattenlängen:

Dh2 = (l'2 : l'1)Dhl

Bei genauen Kartierungen müßen auch die internen Verzerrungen korrigiert werden, die aus der Abweichung von der Lotlinie der Senkrechtaufnahme abzuleiten sind. In einem idealen Nadirbild ohne Relief ist der Bildmaßstab überall gleich; bei reliefbedingten Abweichungen resultiert eine Verzerrung des Maßstabes innerhalb derselben Aufnahme (Abb. 2.3.5). Diese ungünstigen geometrischen Verzerrungen werden durch Vergleiche mit topographischen Paßpunkten (TP's, Ground Control Points) behoben (vgl. auch Kap. 3.3). Streng genommen bleibt jedoch immer ein Restfehler zurück, da die Topographie des Geländes zu weiteren Projektionsverzerrungen führt. Bei deutlicher Überschreitung einer Fehlertoleranz müssen die aufwendigeren Methoden der Photogrammetrie Anwendung finden.

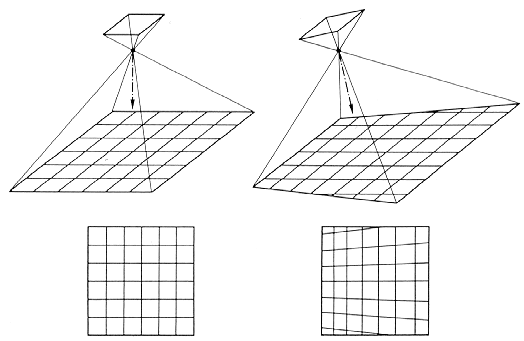Abb. 2.3.5: Schematisierte Maßstabsverzerrung bei Luftbildern (aus Albertz, 1991)

Satellitenbilder mit sehr hoher Auflösung zeigen analoge geometrische Eigenschaften wie Luftbilder! Allerdings treten die radialen Verzerrungen nicht sofort in Augenschein, da die enorme Flughöhe und die i.d.R. geringere geometrische Auflösung der Daten radiale Verzerrungen unterdrücken. Bei großflächigen Aufnahmen oder Weitwinkelobjektiven ist die Erdkrümmung zusätzlich zu berücksichtigen.

Scanner-Bilder oben
Im Gegensatz zur photographischen Aufnahme entsteht das Scanner-Bild i.e.S. nicht vollständig zeitsynchron, also innerhalb eines Augenblicks, sondern fortlaufend, Zeile für Zeile. Für die Geometrie der entstehenden Aufnahme ist dies von entscheidender Bedeutung, da jede Bildzeile streng genommen von einem anderen Ort aus und mit einer etwas anderen räumlichen Lage des Fernerkundungssystems aufgenommen wurde (Perspektive!). Es resultieren Bilder mit wesentlich komplexeren geometrischen Eigenschaften als dies bei der zeitsynchronen photographischen Luftbildgenerierung der Fall wäre.

Grundsätzlich wirken sich drei Faktoren auf die Geometrie der Scanner-Daten aus:

- Aufnahmetechnik (z.B. mechano-optisch oder opto-elektronisch)
- Sensorbewegung (z.B. Art des Orbits bzw. der Fluglage und- bahn)
- Oberflächenform des Geländes (z.B. Flachland oder Gebirge)

Durch die Aufnahmetechnik führen Optisch-mechanische Scanner zu einer typischen Verzerrung des IFOV (Instantaneous Field of View = beobachtetes Flächenelement) hinsichtlich seiner Größe vom Zentrum der Aufnahme zu den Rändern (Abb. 2.3.6). Diese entsteht dadurch, daß der Abstand des Scanners zur Oberfläche im Zentrum der Aufnahme am geringsten ist und dieser zum Rand hin zunimmt. Zugleich dreht sich der Scan-Spiegel mit gleichbleibender Winkelgeschwindigkeit, so daß die Segmente in gleichen Winkel-Inkrementen aufgenommen werden. Bei ihrer Darstellung auf der Basis gleicher Streckenabschnitte kommt es also zu einer Stauchung/Dehnung oder auch zu Panoramaeffekten (geradlinige Strecken wirken am Rande der Aufnahme sigmuidal verkrümmt (Abb. 2.3.7).

Derartige Panorama-Verzerrungen lassen sich mit Hilfe moderner Bildverarbeitungsschritte korrigieren und werden z.T. bereits in der Vorverarbeitung der Daten (preprocessing) durch den Datenvertrieb reduziert. Optoelektronische Scanner verursachen keine Panorama-Verzerrungen (da keine Dreh-Scan-Bewegung: CCD's mit Linsensystem!).

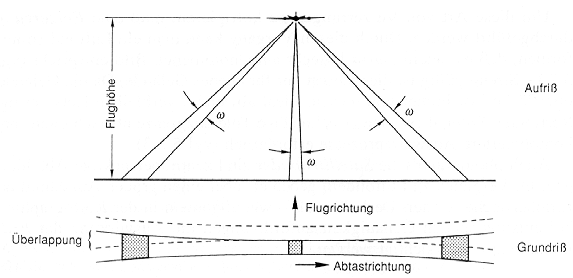Abb. 2.3.6: Schematisierte Verzerrung des IFOV beim optisch-mechanischen Scanner (aus Albertz, 1991)

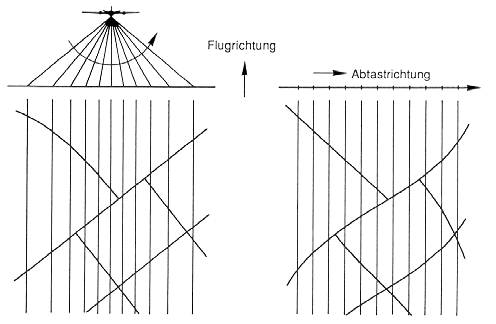Abb. 2.3.7: Typische sigmuidale Panorama-Verzerrung bei Scannerdaten mit Stauchungen und Kompensationseffekten (aus Albertz, 1991)

Hinsichtlich der Flugbahn machen sich alle zeilenweise aufnehmenden Sensoren die Eigenbewegung der Sensorplattform zu Nutze. Satelliten bewegen sich relativ ruhig und stetig in ihrem Orbit, wobei man zwischen polnahen (polaren) und geostationären Umlaufbahnen unterscheidet (Abb. 2.3.8). Es resultieren gleichmäßige Abtastfolgen der Erdoberfläche mit gleichbleibender Verzerrung.

Flugzeugscanner sind hingegen starken atmosphärischen Turbulenzen ausgesetzt; es kommt daher zu ungewollten komplexen 'Roll-Verzerrungen', welche nur schwer zu korrigieren sind. Deshalb werden Flugzeug-getragenen Sensoren auf computergesteuerte, lagestabile Kreisel-Plattformen mit Roll- bzw. Tilt- Kompensation befestigt (Abb. 2.3.9).

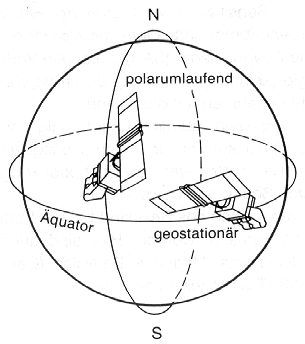Abb. 2.3.8: Typische Satelliten-Orbits (aus Kappas, 1994)

Abb. 2.3.9: Roll-Verzerrungen bei turbulent gestörter Flugbahn eines Flugzeugscanners (aus Albertz, 1991)

Die Oberflächenform des Geländes verursacht in geometrischer Hinsicht bei Flugzeugscannern zusätzliche Komplikationen (wie bei allen hochauflösenden FE-Systemen) . Die mathematisch strenge Korrektur ist nur nach Einbeziehung eines dreidimensionalen Geländemodelles (DGM, vgl. Kap. 3.8) möglich. Diese Vorraussetzungen sind nur in Einzelfällen gegeben, so daß auf geländebedingte Korrekturen oft verzichtet werden muß und nur Näherungslösungen angestrebt werden können. Bei Satelliten bewirken die Oberflächenformen nur in geringem Maße Verzerrungen, da aufgrund der großen Flughöhe und der eher geringeren geometrischen Auflösung keine extremen Lageverzerrungen von Objekten auftreten.

Achtung: FE-Systeme, z.B. Ikonos oder Quickbird, Cartosat) weisen z.T. sehr hohe geometrische Auflösungen von deutlich unterhalb 1m auf! Eine DGM-gestützte Korrektur dieser Satellitendaten wird daher immer wichtiger (vgl. Analogien zu UAV-Daten oder klassischen Luftbildern!).

Meist können die von den Vertriebsorganisationen (z.B. ESA) angebotenen systemkorrigierten Daten direkt ausgewertet werden. Jede genauere Kartierung erfordert jedoch immer eine Geokodierung der Daten auf ein geodätisches Bezugssystem (meist topographische Karten). Durch eine solche geometrische Transformation der Bilddaten über digitale Verarbeitungsschritte wird zugleich die kartographische Abbildung der gekrümmten Erdoberfläche in die gewählte Kartenprojektion vollzogen (z.B. WGS 84, UTM, Gauss-Krüger etc.). Geokodierungen müßen für alle auszuwertenden Fernerkundungsdaten durchgeführt werden, die in ein definiertes Kartensystem überführt werden sollen (Vergleiche auch PP-Beitrag Nr. 2 im praktischen Übungsteil)!

Radar-Bilder oben
Die Bildaufnahme mit Radarsystemen hat in ihrer grundlegenden Form Ähnlichkeit mit der Datengewinnung von Scannern. Die Bilddaten werden aber fortlaufend quer zur Flugrichtung aufgezeichnet (slant range). In Flugrichtung entspricht dies einer Parallelprojektion. In Zeilenrichtung ergibt sich jedoch ein ganz anderes Bild: Lage und geometrische Verzerrung der Flächenelemente ergibt sich vielmehr aus der Laufzeit der Wellenfronten, ihrem Echo und den abgeleiteten Schrägentfernungen der Objekte (Abb. 2.3.10). Für eine ebene Fläche werden die Reflexionssignale entsprechend ihrer Laufzeit (bzw. Schrägentfernung) in Bilddaten umgesetzt, mit der Folge einer zeitbedingten geometrischen Lageverzerrung. Eine nahe gelegene Geländestrecke DY wird von der Wellenfront schneller durchlaufen als eine weiter entfernt - also wird sie im Schrägentfernungsbild verkürzt wiedergegeben und umgekehrt. Diese Verzerrung läßt sich rechnerisch (digital) leicht beheben. Komplizierter wird es jedoch, wenn das Gelände eine ausgeprägte Morphologie besitzt (Abb. 2.3.11).

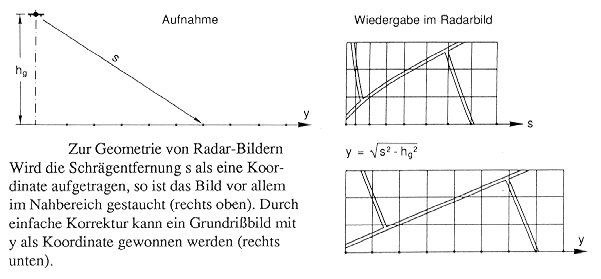Abb. 2.3.10: Schematisierte Geometrie von Radarbildern einer ebenen Fläche (aus Albertz, 1991)

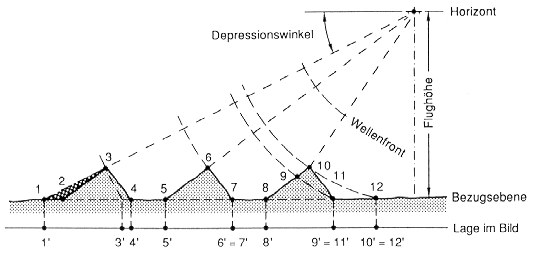Abb. 2.3.11: Auswirkungen des Geländereliefs auf Radarbilder (aus Albertz, 1991)

Erläuterung zu Abb. 2.3.11: Der weitest entfernte Berg wird von der Wellenfront zuerst am Fuße des Berghanges und erst danach am Gipfel getroffen. Die reale Strecke Bergfuß/Berggipfel wird in der Bildbezugsebene um das Projektionsverhältnis von Punkt 4/3 verkürzt dargestellt. Die dem System abgewandte Seite des Berges wird überhaupt nicht wiedergegeben (Radarschatten). Werden Fuß- und Gipfelpunkt gleichzeitig erreicht, kommt es zu einer gleichzeitigen Abbildung der Bildpunkte (layover); wird der Gipfel vor dem Fußpunkt durch die Wellenfront erreicht, kommt es zur Reduzierung der Strecke zwischen den Bildpunkten (foreshortening).

Grundsätzlich werden Geländepunkte, die in einer gemeinsamen Bezugsebene liegen grundrißgetreu abgebildet. Höher gelegene Geländepunkte werden zum Radarsystem hin versetzt dargestellt. Ist der Depressionswinkel größer als die Hangneigung kommt es zu Überlagerungen der Empfangssignale.

Allgemein gilt, daß die Entzerrung von Radarbildern keine triviale Aufgabe ist und nur durch aufwendige Verfahren mit einem erheblichen Maß an Vorkenntnissen auf der System- und Geländeseite gelöst werden kann! Ein DGM ist immer zwingend erforderlich (Meyer & Nüesch, 1986; Wiggenhagen, 1989)!

oben

nächstes Kapitel