
3.1 Digitale Bilder
Allgemeines zur digitalen Bildverarbeitung
Unter digitaler Bildverarbeitung sind all jene Verfahren zu verstehen, welche die Rohdaten der Fernerkundung durch digitale Bearbeitungschritte für eine geowissenschaftliche Interpretation vorbereiten und optimieren. Diese Schritte beinhalten auch das Digitalisieren von Analogdaten, deren Fehlerbereinigung und zielgerichtete mathematische Verarbeitung. Es können so feinste Unterschiede im Bildinhalt mit Hilfe des Rechners verstärkt und ausgewertet werden. Die Interpretation selbst ist streng genommen ein sich anschließender Schritt der Bildverarbeitung, und kann (teil-) automatisiert oder manuell erfolgen.
Die Zielsetzungen, die bei der digitalen Verarbeitung von Bilddaten verfolgt werden sind sehr verschieden. Sie reichen von einfachen Kontrastveränderungen bis zu komplexen Analysen der Bild- oder Spektralsignaturen. Für die Interpretation von Luft- und Satellitenbildern haben sich jedoch eine Anzahl von grundlegenden Operationen bewährt, welche im nächsten Kapitel kurz skizziert werden sollen. Die mathematischen Grundlagen und komplexeren Verfahren werden z.B. von Autoren wie Kraus & Schneider (1988) oder Jähne (1991) bzw. Mather (2004) dargelegt. Momentan wird besonders im Bereich der autonomen Mustererkennung mittels neuronaler Netze und Objekterkennung geforscht. Diese finden teilweise Einzug in objektorientierte Klassifikationsverfahren.
Analoge und digitale Bilder oben
Luft- und Satellitenbilder liegen entweder primär analog (Photo) oder digital (Datenspeicher) vor. Beide Formen können über Digitalisierungs- oder Druckprozessse ineinander überführt werden. Photographische Bilder speichern die Information analog in Form von kontinuierlichen Grau- oder Farbwerten auf der photographischen Schicht. Manipulationen sind eigentlich nur während des Aufnahme- und Entwicklungsprozesses möglich. Digitale Bilder bestehen stets aus matrixnumerisch kodierten Zahlenreihen bzw. -werten, die jederzeit erneut über Programme kopiert bzw. manipuliert werden können.
Man unterscheidet prinzipell zwei Arten von raumbezogenen digitalen Geometriedaten:
- digitale Vektordaten
- digitale Rasterdaten
Digitale Vektordaten können einzeln (Linien) oder verknüpft (Polygone) vorliegen.
Rasterdaten beinhalten unterschiedliche Einzelpixel oder rechteckig angeordnete Pixelhaufen. Beide Datentypen werden neben Attribut- und Metadaten in Geoinformationssystemen miteinander kombiniert (siehe auch Streit, 1997).
In Abbildung 3.1.1 ist die graphische Ausgestaltung der beiden grundsätzlichen Datentypen erläutert.
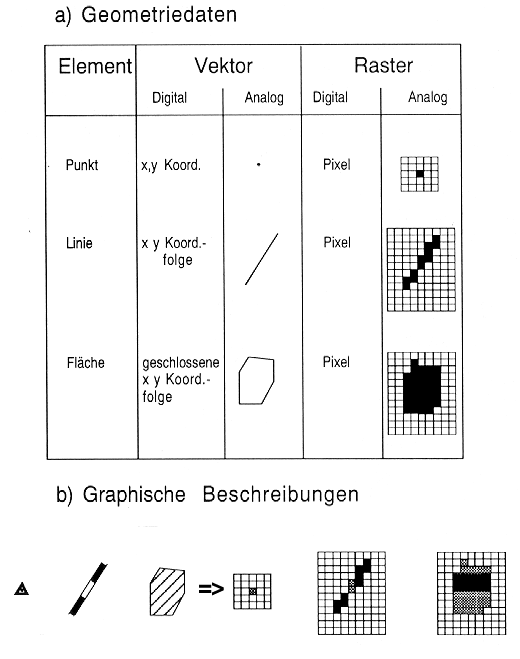 |
Abb. 3.1.1: Geometrie-Rasterdaten und ihre graphische Ausgestaltung in der Fernerkundung (aus Bill & Fritsch, 1994) |
In der Geofernerkundung spielen die Rasterdaten die wichtigste Rolle, da die FE-Sensoren (z.B. Scanner, SAR, digitale Kameras) diesen Datentyp primär generieren. Vektordaten werden bei Bedarf immer erst sekundär dem Datensatz hinzugefügt um linienhafte Geo-Ojekte (Isolininien, Strassen etc.) zu kartographischen oder allg. Geoinformationszwecken zusammen mit ihren Attributinformationen mit den Fernerkundungsdaten zu verschneiden.
Auch photographische Bilder müssen für die digitale Bildverarbeitung digitalisiert, d.h. ihre analoge Information muß in eine numerisch kodierte Rasterform überführt werden. Dieser Prozeß wird Analog/Digital-Wandlung genannt (A/D-Wandlung) und von jedem Scanner durchgeführt (Abb. 3.1.2). Der umgekehrte Weg (D/A) führt zur analogen Bildwiedergabe (z.B. Drucken). Bei der A/D-Wandlung werden photographische Bilder in definierte Geometrieeinheiten zerlegt (Pixel) von dem jede eine Ziffer (Farb- oder Grauwertkodierung, je nach bit-Tiefe) erhält: Das Bild wird aufgerastert! Die Überlagerung mit einem rechteckigen Raster quadratischer Elemente (Abb. 3.1.3) führt zu der Frage, wie eng muß mein Raster sein, damit ich Objekte noch als solche erkennen kann?
Primäre Fernerkundungsrasterdaten (z.B. (E-)TM) besitzen ihre eigene Rastergeometrie (z.B. 180 km x 180 km bei (10) 30m/Pixel ~ 6000 x 6000 Pixel). Analoge Bildvorlagen besitzen eine andersartige Auflösung und müssen deshalb so fein gescannt werden (Rasterweite), daß jedes Objekt im Rasterdatensatz gut erkannt werden kann. Grundsätzlich geht bei der nicht hinreichend feinen Rasterung Information verloren, da Quadrate, die keine vollständige Grauwertausfüllung haben, nicht mit Ziffern belegt werden; die Abbildung wird blockhaft!
Vorbemerkung: Die digitale Grauwertzerlegung von Schwarz (0) nach Weiß (255) führt so zu einer Grauwertspanne von 256 Grauwertstufen (DN-Werte = Digital Number), also 2 exp. 8 = ein Byte (8bit), aber auch 11, 16 oder 32 Bit Fernerkundungsdaten mit bis zu 2exp.32 Grauwertstufen sind zur Verdeutlichung feinster Reflexionsunterschiede in der Anwendung zu verarbeiten.
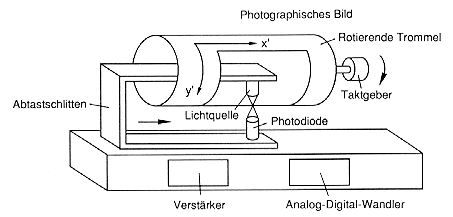 |
Abb. 3.1.2: Prozeß der Digitalisierung über einen Scanner (aus Albertz, 1989) |
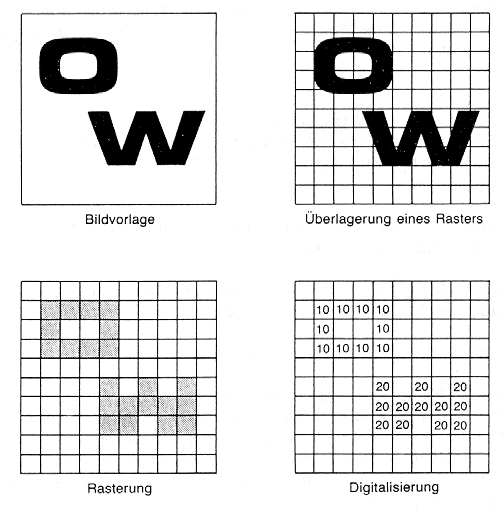 |
Abb. 3.1.3: Prozeß der Digitalisierung (aus Kappas, 1994) |
Bildmatrix digitaler Rasterbilder oben
Jedes digitale Rasterbild - egal ob primär vom Sensor erzeugt oder sekundär von einer analogen Vorlage digitalisiert - weist eine ihr spezifische Bildmatrix auf, welche in einem orthogonalen Koordinatensystem darzustellen ist (Abb. 3.1.4). Bildverarbeitungsschritte können als mathematische Transformationen der Ursprungsmatrix in eine neue Bildmatrix verstanden werden, d.h. durch die Transformationsfunktion wird die zweidimensionale Eingabematrix (x,y) in eine neue zweidimensionale Ausgabematrix (x',y') umgewandelt (diskrete Grauwertfunktion), wobei alle Grauwerte i.d.R. zwischen 0 und 255 liegen.
Insgesamt finden zwei Gruppen von (Grauwert-) Funktionen Anwendung:
- durch geometrische Transformationen werden Bilder in ihrer Form verändert, die ursprünglichen Grauwerte bleiben i.d.R. dabei erhalten (z.B. Entzerrungen)
- durch radiometrische Transformationen werden die Grauwerte verändert, während die geometrischen Eigenschaften erhalten bleiben (z.B. Kontrastverbesserung, unterdrücken von Rauschen)
Eine Bildmatrix besteht immer aus Bildspalten (columns) und Bildzeilen (rows), deren Ursprung meist links oben im Koordinatensystem (Bildschirm) liegt. Ihr Produkt mal Datentiefe ergibt immer die Größe einer Bilddatei (z.B. 10 x 10 Pixel [x 1 byte = 8 bit] = 100 Byte)! Bei Satellitendaten sind die Pixel immer rechteckig (i.d.R. quadratisch) und durch ihre Auflösung pro Pixel definiert (z.B. 10m bei SPOT P-Mode oder 70cm bei Quickbird im P-Mode). Durch Bildverarbeitungsprogramme können diese meist quadratischen Pixel auch in Rechtecke umgewandelt werden, wenn z.B. seitliche Überlappungen vorliegen (z.B. 30 x 25 m/Pixel bei TM).
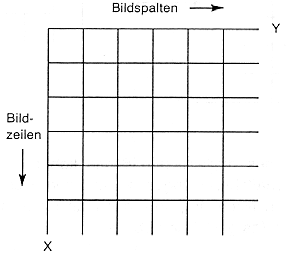 |
Abb. 3.1.4: Einfacher Bildaufbau eines digitalen Rasterbildes (aus Kappas, 1994) |
Ein Bild kann monochrom, panchromatisch (einkanalig) oder multispektral/hyperspektral chromatisch (mehrkanalig) aufgebaut sein (z.B. SPOT P-Mode und SPOT XS-Mode). Im monochromen Fall beschreibt ein Pixel P(z,s) die Zeile z und die Spalte s mit einem bestimmten Grau- oder DN-Wert (Abb. 3.1.6). Die Abbildungstiefe liegt hier bei 8 bit (schwarz/weiss entsprechend 1 bit).
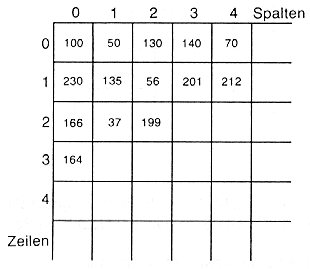 |
Abb. 3.1.5: Bildmatrix eines monochromen Bildes mit Grauwerten/Pixel (aus Kappas, 1994) |
Im multispektralen Fall ist ein farbiges Bild als Summe aus mehreren Kanälen anzusehen; das Pixel P(k,z,s) beschreibt deshalb die Position mit einem Grauwert in einem bestimmten Kanal. Die Anzahl der zu Farbaufnahmen zusammengefügten Kanäle ist immer gleich 3, da sich das RGB-Farbsystem aus drei Farbkomponenten zusammensetzt (s.u.). Die Abbildungstiefe liegt hier bei 3 x 8 bit = 24 bit.
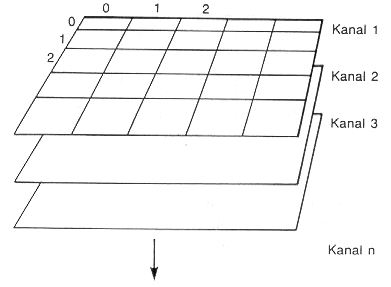 |
Abb. 3.1.6: Bildmatrix eines multispektralen (hier dreikanaligen) Bildes (aus Kappas, 1994) |
Zu den Methoden der digitalen Bildverarbeitung gehören neben den oben beschriebenen zwei Grundtypen auch die Integraltransformationen im Frequenzbereich (z.B. Filterungen, FFT). Diese interpretieren ein Bild als Überlagerung von Schwingungen unterschiedlicher Grauwert-Frequenzen welche gefiltert werden können und so bestimmte Kontraststrukturen gerichtet herausfiltern können (s.u.).
Anforderungen an den Rechner oben
Für viele digitale Bildverarbeitungsschritte sind komplexe und damit zeit-/rechenintensive Operationen notwendig. Die Rechner sollten deshalb über genügend schnelle CPU's (Central Processing Unit), sehr grossen Arbeitsspeicher und Festplattenplatz verfügen. Entsprechendes gilt für vernetzte Speicherkapazitäten/Cloud-Systeme, da Fernerkundungsdaten erfahrungsgemäß sehr gross sind und bei jeder Operation neue Daten errechnet und abgelegt werden müssen (eine multispektrale Satellitensze umfaßt u.U. mehrere GByte, Luftbildreihen/hyperspektrale Daten bis zu mehrere TByte!). Im Laufe eines FE-Projektes erreicht man so leicht riesige Datenmengen, die es auch parallel zu verwalten gilt (inkl. Sicherheitskopien!).