3.6 Filterungen
Zielsetzung
Jedes rasterbasierte Bildverarbeitungssystem besitzt als Grundfunktionen der Bildaufbereitung auch digitale Filterungsroutinen. Diese stellen komplexe räumliche Pixeloperationen dar (engl.: spatial enhancement), da sie den DN-Wert eines einzelnen Pixels abhängig von seiner räumlichen Pixelumgebung verändern - im Gegensatz zum radiometric enhancement, welches Pixelwerte z.B. über Histogramm-Streckung neu berechnen.
Die Wirkungsweise von Filtern kann sehr verschieden sein. Viele Bildverarbeitungssysteme bieten aber eine Reihe von Standardfiltern an, zu denen sich zusätzlich weitere Filter interaktiv editieren lassen.
Für die digitale Filterung ergeben sich erfahrungsgemäß vier Hauptanwendungsgebiete:
- allgemeine Bildverbesserung
- Bildentzerrung
- Extraktion von geometrischen Bildinhalten
- Mustererkennung
Grundsätzlich dient als räumlicher Filter eine Koeffizientenmatrix, mit deren Hilfe ein kleiner Bereich des Eingabebildes auf einem einzelnen Bildpunkt des Ausgabebildes abgebildet wird. Der Filter muß dann über das ganze Bild 'laufen' und das Eingabebild mathematisch 'falten' (Abb. 3.6.1).
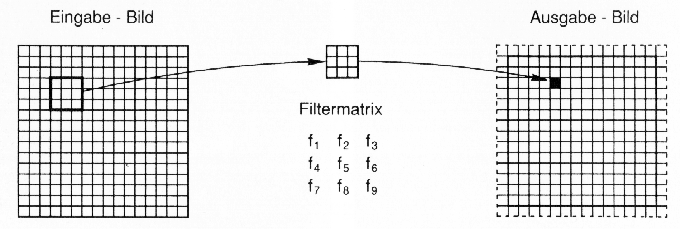 |
Abb. 3.6.1: Schematische Darstellung der Filterung. Ein kleiner Bereich des Eingabebildes wird mit dem Koeffizienten einer Filtermatrix (hier 3 x 3 ) zu einem neuen, einzelnem Pixel verrechnet (Albertz, 1991) |
Prinzip der digitalen Filterung oben
In der digitalen Bildverarbeitung wird ein Bild als zweidimensionales Signal dargestellt (Signal = G[x,y]). G ist der Grauwert als Maß der aufgenommenen reflektierten bzw. emittierten Strahlungsintensität. Die x- und y-Werte sind ganzzahlige (integer) Ortsvariablen von G (Abb. 3.6.2).
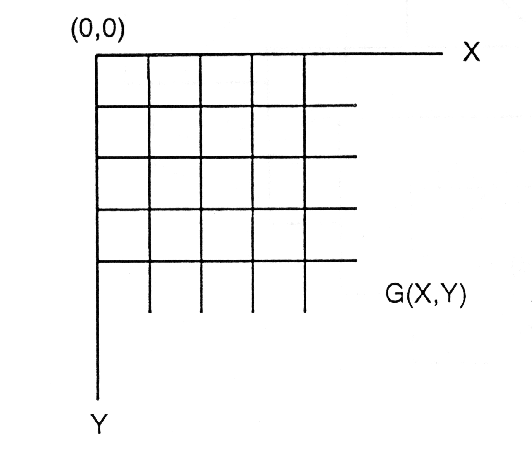 |
Abb. 3.6.2: Schematische Darstellung der eines einkanaligen, zweidimensionalen Bildsignales (Kappas, 1994) |
Der Wertebereich von G liegt zwischen 0 und 255 (entsprechend 8-bit binär = 1 byte); normalerweise wird die Zuordnung 255 = Weiss und 0 = Schwarz getroffen. Für farbige Darstellungen kommen im RGB-System noch zwei weitere Dimensionen hinzu, aber auch n-dimensionale Filter sind denkbar.
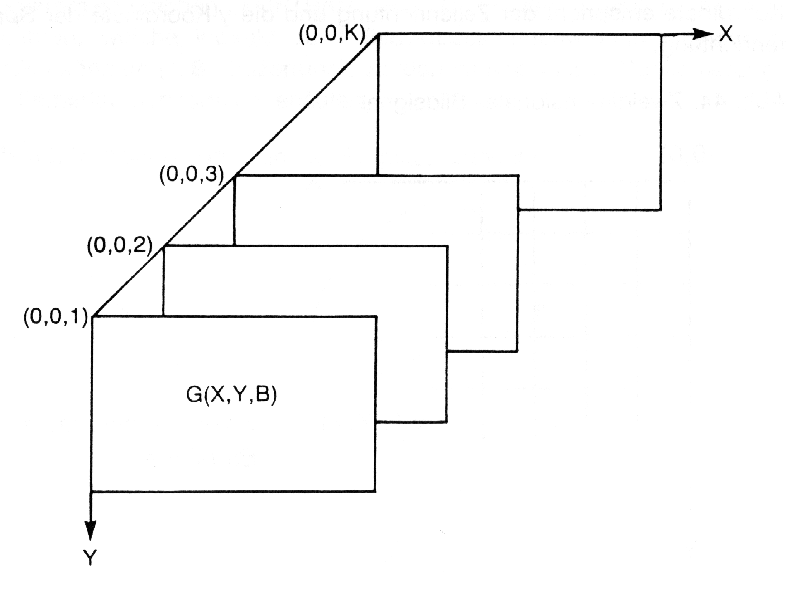 |
Abb. 3.6.3: Schematische Darstellung der eines drei- bis multikanaligen, zweidimensionalen Bildsignales (Kappas, 1994) |
Neben der räumlichen Filterung von digitalen Bilddaten im Ortsbereich kann auch eine Filterung der (räumlichen) Frequenz (engl.: spatial frequency) des Bildes erfolgen. Man versteht unter der räumlichen Frequenz den Unterschied zwischen den höchsten und niedrigsten Werten einer kontinuierlichen Folge von Pixeln. Jensen (1986) definiert sie als die Anzahl/Amplitude der Helligkeitsveränderungen pro Raumeinheit in einem bestimmten Teil des Bildes (Abb. 3.6.4).
Möglich sind:
- keine räumliche Frequenz des Bildes; d.h. flaues, kontrastloses Bild mit weitgehend Einheits-DN-Werten
- geringe räumliche Frequenz des Bildes; d.h. sanfte Übergänge im Kontrast
- hohe räumliche Frequenz des Bildes; d.h. extreme Kontraste (Muster) zwischen den Pixelgruppen
 |
Abb. 3.6.4: Schematische Darstellung der räumlichen Frequenz von Rasterdaten (ERDAS, 1997) |
Die Darstellung der räumlichen Frequenz eines Bildes wird i.d.R. über eine Fouriertransformation in x- und y-Richtung vollzogen. Dabei geht man davon aus, daß jede stetige Kurve durch eine unendliche Summe von Kosinus- und Sinusfunktionen dargestellt werden kann. Die genaue mathematische Ableitung der Funktionen kann bei Haberäcker (1989) oder Jähne (1991) nachgelesen werden. Abbildung 3.6.5 zeigt die Beziehung von Signalen im Orts- (Rasterwerte) und Frequenzbereich (Amplitudendurchgang/Zeit) eines Bildes.
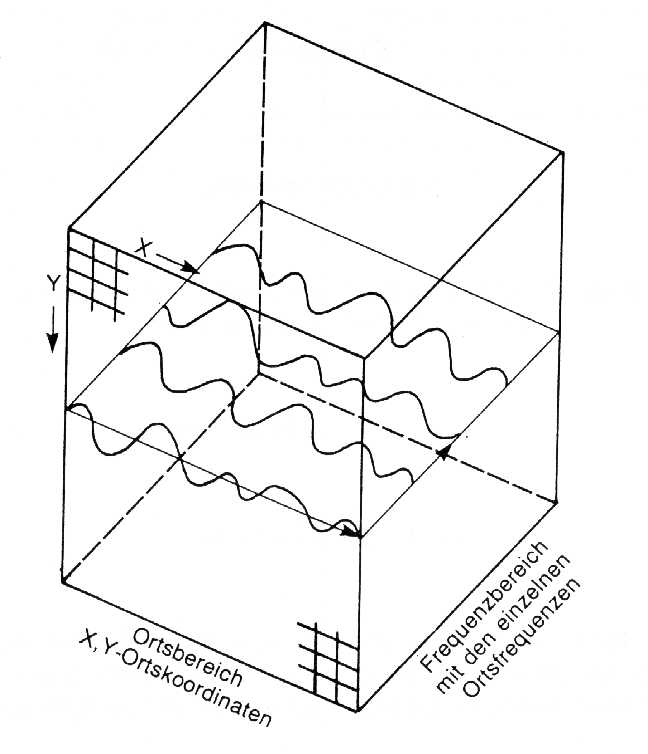 |
Abb. 3.6.5: Schematische Darstellung der räumlichen Beziehung von Frequenz- und Ortsbereich von Rasterdaten (Kappas, 1994) |
Der Ablauf der Filterung eines Bildes im Frequenzbereich durch eine Fast-Fourier-Transformation (FFT) läßt sich durch drei Arbeitsschritte beschreiben:
1. zweidimensionale FFT des Bildes zur Erfassung der (räumlichen) Frequenz
2. Multiplikation des Frequenz/Spektrums mit der zielgerichteten Filterfunktion
3. zweidimensionale, inverse FFT des gefilterten Spektrums in ein Bild mit Ortskoordinaten/neuen DN-Werten der neuer Pixel.
Die FFT findet oft in Kombination mit Hochpaß- und Tiefpaßfiltern oder in texturbasierten Klassifikationsansätzen Anwendung.
Häufige Filtertypen oben
Zur Modifikation des Bildes im Orts- und z.T. auch im Frequenzbereich gibt es unterschiedliche Filtertypen, wobei meist jeder Typ seine spezielle Zielsetzung hat. Für Operationen im Ortsbereich sind besonders Filtermatrizen (engl. kernel) in den Größen 3 x 3, 5 x 5 oder 7 x 7 geeignet. Am bekanntesten sind sicherlich Hoch- oder Tiefpaßfilter, die zu einer Datenverschärfung bzw. -glättung führen, da sie nur hochfrequente oder tieffrequente Bildanteile verstärken. Die Funktionsweise eines 3 x 3 Hochpaßfilters soll an folgendem Beispiel erläutert werden (Abb. 3.6.6):
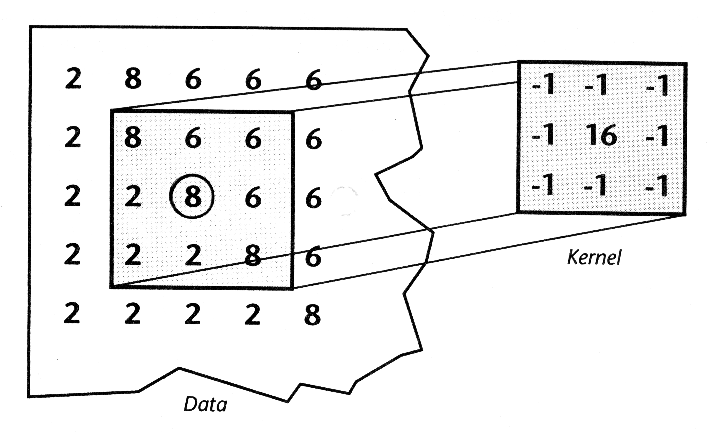 |
Abb. 3.6.6: Schematische Darstellung der Wikungsweise eines 3 x 3 Hochpaßfilters auf ein Rasterbild (ERDAS, 1997) |
Um den Ausgabewert für das erste Pixel (8, links oben!) zu errechnen wird jeder Matrixwert mit seinem korrespondierenden Pixelwert multipliziert und anschließend aufsummiert.
Dieser Wert wird dann durch die Summe der Matrix-Koeffizienten geteilt (Wertigkeit der Matrix immer ungleich 0!); d.h.:
integer (-1 x 8) + (-1 x 6) + (-1 x 6) + (-1 x 2) + (16 x 8 ) + .......... / (-1 + -1 + -1 + -1 + 16 +....) = ((128 - 40) / (16 - 8)) = (88 / 8) = 11 = neuer DN-Wert!
Nach der Filterung stellt sich das Ausgabebild wie folgt dar:
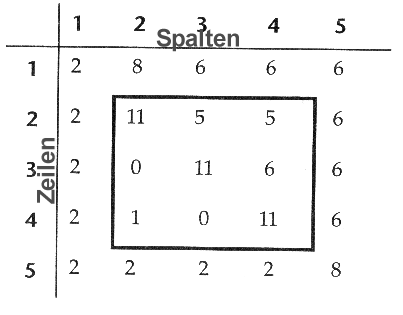 |
Abb. 3.6.7: Resultat des 3 x 3 Hochpaßfilters auf das Rasterbild aus Abb. 3.6.6 (ERDAS, 1997) |
Wichtig: Man beachte, daß die Randpixel nicht in die Filterung miteinbezogen wurden (fehlende Pixelnachbarn)!
Aus der Vielzahl der möglichen Filter seien hier einige bekannte Typen kurz skizziert.
- der Tiefpaßfilter, z.B. zur Dämpfung eines Bildes
| 1 | 1 | 1 | |
| 1 | -16 | 1 | |
| 1 | 1 | 1 |
- der bewegte Mittelwertfilter, z.B. zur Glättung eines Bildes
| 1 | 1 | 1 | |
| 1 | 1 | 1 | |
| 1 | 1 | 1 |
- der Sobel-Filter, z.B. zur Extraktion von Kanten (nach Richtungen)
| 2 | 3 | 2 | |
| 0 | 0 | 0 | |
| -1 | -2 | -1 |
- der Laplace-Filter, z.B. zur allgemeinen Extraktion von Kanten
| 0 | 1 | 0 | |
| 1 | -6 | 1 | |
| 0 | 1 | 0 |
Um starke Grauwertunterschiede in einem Bild zu glätten, wird oft der bewegte oder gleitende Mittelwert benutzt (engl.: moving average). Dieser mathematisch einfache Operator nähert Grauwertübergänge in einem Bild an, so daß das Ausgabebild etwas unschärfer gegenüber dem Originalbild erscheint (Abb. 3.6.8). Er funktioniert also ähnlich wie ein Tiefpaßfilter, der ja hohe Frequenzen glättet und zu einem weicheren Bild führt; insbesondere werden Kanten unterdrückt. Vergleichbare Folgen haben auch Median-Filter, welche die Grauwerte der Größe nach sortieren und den zentralen Wert als neuen Ausgabewert definieren. Besonders wichtig sind die kantenverstärkenden Sobel- oder Laplace-Operatoren, mit deren Hilfe lineare Strukturen verstärkt werden können (Raster-Vektor-Konvertierung!). Dabei sind auch Richtungen mit dem Filter detektierbar (Abb. 3.6.9).
 |
Abb. 3.6.8: Resultat des 3 x 3 Mittelwert-filters auf ein TM-Rasterbild von Louisville |
 |
Abb. 3.6.9: Resultat eines ungerichteten Sobeloperators auf ein TM-Rasterbild von Münster |
Neben den oben kurz skizzierten Filtern gib es noch eine große Anzahl sehr spezieller Filter, wie z.B. den Prewitt-Operator zur richtungsabhängigen Filterung von Zeilen und Spalten (Kompaßgradienten), den Crisp-Filter zur teilweisen Beseitigung von Unschärfen (z.B. atmosphärischer Dunst), den Speckle-Filter zur Reduzierung von Rauschen im SAR-Bild usw..
Auch Klassifikationsergebnisse können ggf. durch Filteroperationen optimiert werden, sofern punktuelle Fehlklassifikationen vorliegen; hier werden meist glättende Kernel verwendet.
Zum Abschluß des Kapitels soll noch auf den Einsatz von Filter während der Frühphase der Datenaufbereitung hingewiesen werden. In einigen Fällen sind Datensätze nur unvollständig und mit systematischen Störungen von Satelliten an die Empfangstation übermittelt worden. Diese Empfangsstörungen drücken sich meist in fehlerhaften Zeilen oder Spalten bzw. einem typischen Scan-Rauschen (noise) aus. Mit dem Einsatz gerichteter Mittelwert-Filter können diese Datenfehler weitgehend behoben werden (remove bad lines/columns) oder durch Bandpaßfilterung bzw. Bandsperre korrigiert werden (de-striping). Im ersten Fall werden nicht oder fehlerhaft besetzte Zeilen und Spalten durch die Mittelwerte ihrer Pixel-Umgebung besetzt (Abb. 3.6.10); im zweiten Fall werden bestimmte Frequenzen aus- oder eingeblendet (Abb. 3.6.11).
Resultat eines gerichteten Mittelwertfilters zur Korrektur fehlerhaft besetzter Spalten in einem Rasterbild:
fehlerhafte Matrix (Eingabebild):
| 2 | x | 6 | |
| 2 | x | 4 | |
| 2 | x | 2 |
Mittelwert-korrigierte Spalte (Ausgabebild):
| 2 | 4 | 6 | |
| 2 | 3 | 4 | |
| 2 | 2 | 2 |
|
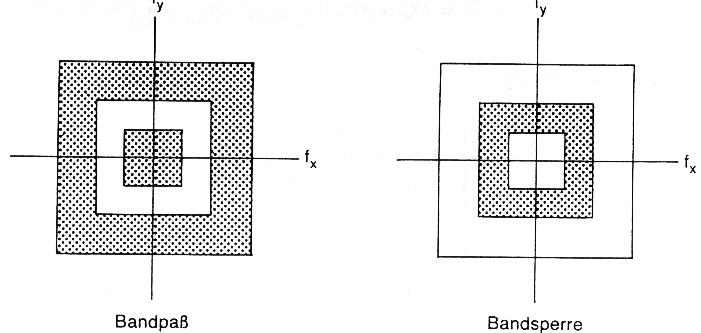
Abb. 3.6.11: Schematische Funktionsweise einer Bandpaßfilterung und einer Bandsperre; schraffierte Bereiche (Frequenzen) werden unterdrückt (Kappas, 1998) |
Zur weiterführenden Vertiefung seinen hier auf die Veröffentlichungen von Kraus & Schneider (1988), Haberäcker (1989), Kraus (1990) und Jähne (1991) hingewiesen. Darüber hinaus sollte in dem Anhang eines jeden Software-Handbuches der digitalen Bildverarbeitung eine detailierte Erläuterung der mathematischen Filterfunktionen des benutzten Programmes zu finden sein.