
3.3 Geokodierung
Die Geokodierung (geocoding) oder auch 'geometrische Entzerrung' von Fernerkundungsdaten ist mit geometrischen Operationen verbunden, die das digitale Bildmaterial in einen geographischen Raumbezug stellen. Dies ist insbesondere immer dann notwendig, wenn die Fernerkundungsdaten in ein geographisches Informationssystem (GIS) integriert werden sollen.
Was ist Geokodierung?
Vereinfacht beschreibt der Vorgang der Geokodierung die Prozesse, welche eine geometrische Transformation der Originaldaten mit internem Bild-Koordinatensystem in ein gewähltes geodätisches Bezugssystem (z.B. Kartenprojektionen) unter weitgehender Eleminierung der system- oder geländeabhängigen Verzerrungen erlauben. Bilddaten sind dann als geokodiert zu bezeichnen, wenn jedem Pixel eine exakte (x, y, ggf. auch z) kartographische Koordinate zugeordnet werden kann. Üblicherweise wird immer ein geodätisch/kartographisches Referenzsystem gewählt um die quantitative Analyse sowie weitere Exportmöglichkeiten der Bilddaten in topographische Karten oder andere Programme zu ermöglichen.
Der eigentliche Transformationsprozeß kann durch die Methoden der digitalen Bildverarbeitung sehr flexibel gestaltet werden. Die grundlegenden Elemente sind jedoch immer drei Arbeitschritte (vgl. auch Praktikum!):
- Die geographische Abbildungsgeometrie muß definiert werden (z.B. UTM oder Gauss-Krüger)
- Die Verzerrungen werden aus dem Bild über polynomische bzw. parametrische Modelle mit Hilfe von gemeinsamen Paßpunkten in der Kartenvorlage/Bilddaten zurückgerechnet
- Die eigentliche Berechnung/Transformation der x,y-Koordinaten für jedes Pixel im neuen Bezugssystem wird unter Beibehaltung oder Neuberechnung der radiometrischen Information (Grauwert) von Bildpunkt zu Bildpunkt durchgeführt
Jede genaue Entzerrung setzt vorraus, daß genügend Paßpunkte (ground control points = GCP's) zur Verfügung stehen. Darunter versteht man Punkte, die sowohl im Bild als auch in der Karte eindeutig zu lokalisieren sind. Mit Hilfe dieser identischen Paßpunkte in Karte und Bild kann die geometrische Beziehung zwischen Pixel und Geländepunkt hergestellt werden (z.B. x,y im Bild zu Rechts- und Hochwert in der Karte). Ihre Auswahl muß mit größter Sorgfalt getroffen werden, denn von ihrer Lagebestimmung hängt die Qualität der Entzerrung ab! Die Transformation wird dann über sogenannte Ausgleichspolynome vorgenommen. Theoretisch kann man zwischen folgenden Paßpunkttypen unterscheiden:
- Lagepaßpunkt (x,y-Koordinate bekannt)
- Höhenpaßpunkt (z-Koordinate bekannt)
- Vollpaßpunkt (x,y,z-Koordinate bekannt)
In der Praxis finden meist Lagepaßpunkte Anwendung. In der Photogrammetrie sind jedoch genaue Vollpaßpunkte zur Erzeugung von Ortho-Abbildungen (z.B. Orthophotos) notwendig. Die Auswahl der Punkte ist natürlich durch die Auflösung und den Maßstab der Bilddaten eingeschränkt. Sehr gut eignen sich z.B. Straßenkreuzungen, markante Geländepunkte, Eisenbahnlinien, größerer Gebäudekomplexe o.ä.. Die Bildkoordinaten der Paßpunkte werden üblicherweise interaktiv am Bildschirm abgegriffen und mit den geodätischen Koordinaten verknüpft. Wenn kein Kartenmaterial zur Verfügung steht, muß ggf. mit GPS-Punkten, welche zuvor im Gelände aufgenommen worden sind, gearbeitet werden. Weiterhin ist die Einbeziehung bereits georeferenzierter, sekundärer FE-Daten oder vordefinierter Passpunkt-Dateien möglich.
Auswahl der Paßpunkte oben
Eine Auswahl von guten Paßpunkten gestaltet sich in der Praxis oft schwierig, da selbst auf den ersten Blick einfach zu lokalisierende Punkte im Bilddatensatz nur sehr ungenau (d.h. über zwei bis drei Pixel verschwommen; bei TM bedeutet dies ggf. bereits 90 m!!) als Mischsignatur zu erkennen sind. Eine ständige Optimierung ist deshalb schon bei der Auswahl zu treffen und wird von vielen Programmen über eine Zwischenfehlerberechnung (Root Mean Square Error) erleichtert.
Zusätzlich müßen hinreichend viele Punkte in einer geometrisch sinnvollen Anordnung gefunden werden: Die Anzahl der Paßpunkte steuert den Grad der affinen Transformation (d.h. Maßstabsanpassung, Drehung und Translation)! Für ein Polynom 1.Grades werden mindestens 3 Punkte benötigt (Fläche!), für den 2.Grad 6 Punkte (Paraboloid!), für den 4.Grad 10-15 usw. (komplexere perspektivische Verzerrungen!).
Grundsätzlich sollten immer deutlich mehr Punkte gesucht werden, als mathematisch zwingend notwendig, da durch die ständige Qualitätskontrolle einige Punkte nachträglich verworfen werden müssen. Grundsätzlich sollten die Punkte auch nicht irgendwo gehäuft auftreten, sondern gleichmäßig über das ganze Bild verteilt sein! Insbesondere der Bildrand ist gut abzudecken, da hier i.d.R. die größten Verzerrungen (hohe Anteile der optischen Zentralprojektion!) auftreten!
 |
Abb. 3.3.1: Interaktive Auswahl von Paßpunkten (GCP) unter ERDAS zur Rektifizierung eines JERS-Datensatzes von Hiddensee (Ostsee) |
Ein Problem des obengenannten Vorhehens ist dabei oft schon der Zeitaufwand, der für die eigentliche Markierung der Paßpunkte in der Karte und dem zu rektifizierenden digitalen Bild benötigt wird: Für eine Satellitenszene mittlerer geometrischer Auflösung (z.B. Landsat ETM) sollten mindestens 30-50 Punkte bestimmt werden, damit eine hinreichende Genauigkeit erreicht wird. Die Kartengrundlage sollte im Maßstab nicht kleiner als 1: 50.000 vorliegen um den zeichnerischen Lagefehler einer starken Objekt-Generalisierungen nicht auf die digitalen Daten zu übertragen (Beachte: Im Maßstab 1: 100.000 übertrifft die Signatur einer Straße ihre tatsächlichen Ausmaße bereits um das 15-fache!!).
Die theoretische Lagegenauigkeit von Objekten auf einer Karte läßt sich nach Kappas (1994), ausgehend von der Zeichengenauigkeit und dem Maßstab, jederzeit bestimmen:
Theor. Lagegenauigkeit = Zeichengenauigkeit x Maßstab / 1.000 m
Bsp.: Für eine Karte im Maßstab 1: 25.000 liegt die Zeichengenauigkeit bei etwa 0,2mm; daraus ergibt sich eine theor. Lagegenauigkeit von nur +/- 5m!
Im Idealfall sollten Karten/Referenzbilder im Maßstab 1: 5.000 oder 1: 10.000 bzw. max 1:25.000 gewählt werden.
Neben den oben genannten Fehlerquellen kommt in Regionen mit stark entwickeltem Relief (Gebirge!) noch der planimetrische Fehler (ähnlich der Radialverzerrung bei Luftbildern) hinzu. Dieser Fehler kann nur unter Zuhilfenahme von Höhendaten, z.B. eines DGM's (Digitales Höhenmodell) korrigiert werden und kann u.U. bei etwa der Hälfte der geometrischen Auflösung liegen. Oft wird bei Satellitendaten mangels DGM's auf seine Korrektur verzichtet, da keine genauen Z-Werte abgegriffen werden können.
Wahl des Entzerrungsprozesses/Resampling oben
Die meisten Satellitendaten sind bereits von ihren Vertriebsinstitutionen systemkorrigiert worden, so daß sofort mit einer indirekten Transformation des Bildinhaltes auf eine geodätische Grundlage begonnen werden kann. In der Praxis reichen hier Polynome 1.- 3.Ordnung aus.
Nach der Bildoptimierung und genauen Bestimmung der Paßpunkte wird zunächst das Entzerrungspolynom festgelegt; d.h. es soll für jedes Pixel des entzerrten Ausgabebildes die Position und der Grauwert des zu übertragenden Pixels (verzerrtes Bild) berechnet werden (Abb. 3.3.2).
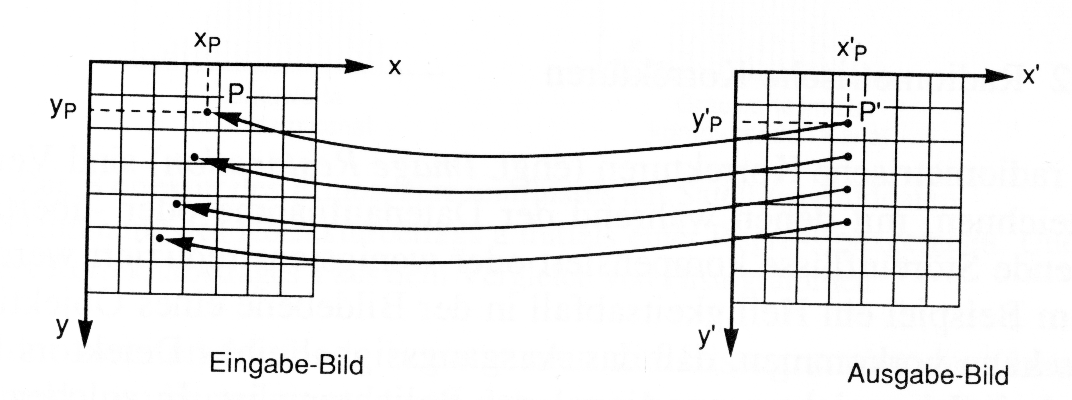 |
Abb. 3.3.2: Indirekte Entzerrung - Für die Elemente des Ausgabebildes werden die Grauwerte (gerade Strecke!) im Eingabebild gesucht (aus Albertz, 1991) |
Für die eigentliche Transformation stehen i.d.R. drei gängige Zurückverteilungsmethoden oder Resampling-Methoden zur Verfügung (vgl. Praktikum!):
- Das Verfahren der 'nächsten Nachbarschaft' (nearest neighbour) ist das am weitesten verbreitete Resampling-Verfahren. Es wird bevorzugt angewandt, wenn eine nachfolgende Klassifikation der Daten geplant ist. Bei dieser Methode wird der Grauwert jenes Pixels im Eingabebild übernommen, welches den berechneten neuen Koordinaten x' und y' am nächsten liegt. Die Eingabegrauwerte der Pixel bleiben dabei erhalten! Das Verfahren benötigt am wenigsten CPU-Rechenzeit führt aber u.U. zu 'blockigen' Bildern
- Die Methode der bilinearen Interpolation (bilinear interpolation) betrachtet die Grauwerte einer Zweierumgebung in der nächsten Zeilen- und Spalten-Nachbarschaft. Das Verfahren ist etwas aufwendiger als die N.N.-Methode, erbringt aber akzeptable Ergebnisse ohne blockige Bildformen. Allerdings werden hier die Grauwerte neu berechnet (i.d.R. gemittelt/interpoliert)!
- Die 'kubische Faltung' (cubic convolution) verwendet eine Art Hochpaßfilter in der Größe von 4 x 4 Pixeln um eine Interpolation höherer Ordnung durchzuführen; dabei werden die Grauwerte des Ausgabebildes über die Matrix neu berechnet. Die Ergebnisse der kubischen Faltung sind bzgl. der Lagegenauigkeit sehr gut, allerdings steht ihr hoher Rechenaufwand dem praktischen Einsatz für große Datenmengen gegenüber (ca. 7 x langsamer als N.N.-Meth.)
Häufig wird das Resampling-Verfahren nach der Nearest Neighbour-Methode angewandt, da hier ein ausgewogenes Verhältnis von Rechenzeitaufwand zu Ergebnis erreicht wird (Abb. 3.3.3) und die Originalgrauwerte unverändert bleiben. Letzteres ist besonders für später durchzuführende Klassifizierung der Daten von Vorteil.
  |
Abb. 3.3.3: Verzerrtes und geographisch rektifiziertes KVR-1000 Bild der Nordspitze Hiddensees |
Darüber hinaus ist es für viele praktische Aufgaben erforderlich, mehrere, aber unterschiedlich referenzierte digitale Satelliten- oder Luftbilder miteinander zu verschneiden bzw. zu verknüpfen. Die Bildung von Daten-Mosaiken (mosaicing, stiching) oder der Verschneidung von unterschiedlichen geometrischen Auflösungen (resolution merge) wird ähnlich gelöst (vgl. Kap. 3.5). Hierbei finden häufig Re-projektionen/Umreferenzierungen, automatischen Bildverknüpfungsmethoden wie automatisierte Grauwert-Mustererkennung und Verknüpfungspunkt-Generierung (automated tie-points) als auch 'structure from motion' (SFM) Strategien (z.B. bei Drohnendaten) Anwendung.