3.8 Digitale Geländemodelle (DGM)
DGM's und FE-Daten
Die zahlenmäßige Beschreibung der dreidimensionalen Oberflächenform eines Geländes in alphanumerischer Form durch die Raumkoordinaten x, y, z einer ausreichenden Menge von Punkten der Objektoberfläche wird als digitales Geländemodell (DGM, oder DTM = Digital Terrain Model bzw. DEM = Digital Elevation Model oder auch DHM = Digitales Höhenmodell) bezeichnet. Als Bezugssystem dient dabei ein Geländekoordinatensystem, i.d.R. das Landeskoordinatensystem (Hildebrandt, 1996). Ist man stärker an der eigentlichen Oberfläche (z.B. Vegetationshöhe) interessiert, spricht man von einem digitalen Oberflächenmodell (DOM).
Die Generierung digitaler Geländemodelle (sei es nun aus stereoskopischen UAS-/Luft- bzw. Satellitendaten, Laser-Altimetrie (LIDAR) oder aus bereits bestehenden topographischen Karten) hat für die digitale Auswertung von FE-Daten zunehmend an Bedeutung gewonnen. Wo zunächst nur der Wunsch nach einer möglichst naturgetreuen Abbildung der Landschaft (virtuelle Geländeformen) stand, finden sich heute hohe Ansprüche an die Genauigkeit des aus FE-Daten abgeleiteten Modells selbst, da aus ihm wichtige geowissenschaftliche Zusatzinformationen generiert werden können, die für viele Aufgabenstellungen eine Planungsrelevanz besitzen (z.B. Hangneigung und -exposition, Erosionsgefährdung, Entwässerungssysteme, Einzugsgebiete etc.). So lassen sich z.B. durch die Verknüpfung von DGM, FE-Daten und aus ihnen abgeleitete Klassifizierungen Aussagen über den geomorphologischen Hintergrund einer Flächennutzungsart oder bestimmter physiogeographischer Gegebenheiten treffen.
Prinzipiell können digitale DGM's auf unterschiedliche Art und Weise erzeugt werden. Die beiden häufigsten Methoden sind:
- Digitale orthophogrametrische Auswertung stereoskopischer Bildpaare (3D Aerotriangulation von UAS-/Luft- oder Satellitenbildern)
- Digitalisierung von analogen Informationen/Isolinien aus bestehenden historischen topographischen Karten
- Radar- oder Laserinterferrometrie/-altimetrie (z.B. LIDAR)
Erstere Methode enstammt der Orthophotogrammetrie mittels Luftbildmessung. Sie ist sehr aufwendig und erbringt aber bei hoher geometrischer Auflösung sehr genaue Ergebnisse. Diese Methode kann auch auf UAV-gestützte Bildpaare angewand werden, wenn die Aufnahmen weitgehend verzerrungsfrei und kalibrierbar sind. Aus stereoskopischen Satellitenaufnahmen (z.B. SPOT, ASTER oder JERS) lassen sich auch DGM's ableiten - diese sind jedoch nur von begrenzter Genauigkeit! Eine Digitalisierung von Höhenlinien auf der Basis bestehender topographischer Karten ist in manchen Fällen (je nach Maßstab!) genauer und dann der stereoskopischen Satellitenbildauswertung vorzuziehen.
Aktuelle Trends setzten jedoch zunehmend auf direkte Höhenmessung mittels Structure from Motion (SfM) Auswertung von Drohnendaten (UAS-3D-Punktwolken); Reflexions-Laufzeitdifferenzen in der Mikrowellen (Radar) oder der Laseraltimetrie (LIDAR).
DGM aus Stereoaufnahmen oben
Ein DGM läßt sich stereophotogrammetrisch erzeugen. Die Entwicklungen der analytischen und digitalen Photogrammetrie und dazugehörender Software (z.B. Pix4D, AGISOFT, OpenDoneMap (ODM), insbesondere im Kontext eines UAS-Bildmosaikflugs oder LPS von ERDAS Imagine) haben dabei weitergehende Möglichkeiten für die automatisierte Herleitung von Punktwolken und Modellen eröffnet.
Die Herleitung erfolgt grundsätzlich in mehreren Schritten:
- Festlegung der notwendigen Datendichte/-struktur
- Datenerfassung (Primärdaten)
- Höheninterpolation, Aerotriangulation
- Berechnung des Modells und seine Manipulation
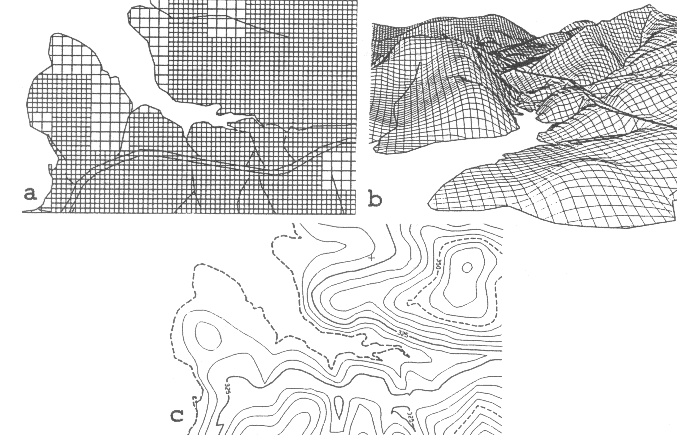
Die Datenstruktur eines Oberflächenmodells wird fast immer über ein quadratisches Punktgitter bzgl. der Höhenmessung definiert (Abb. 3.8.1). Jeder Gitterpunkt ist durch seine Lage (x, y, z) festgelegt.
|
Abb. 3.8.1: Datenstruktur eines DGM (a), seine perspektivische Ansicht (b) und das resultierende Höhens-chichtmodell (c) (Hildebrandt, 1996) |
Um die Oberflächengestalt möglichst genau zu modellieren, werden Netzdichte und Punktmenge von der Reliefintensität und dem Verwendungszweck beeinflußt. Je dynamischer das Relief, desto größer muß die Punktmenge pro Flächeneinheit sein. Bei gleichmäßig ebenen oder nur schwach gegliedertem Relief genügen wenige Gitterpunkte, zwischen denen i.d.R. linear interpoliert wird. Die Generierung der Gitterpunkte erfolgt bei stereoskopischen Aufnahmen durch die Ermittlung des Z-Wertes für jeden Gitterpunkt mit seiner Lage im Bild- oder Referenzkoordinatensystem (x,y). Diese Messung erfolgt entweder gleichmäßig punktuell und/oder zusätzlich entlang wichtiger Profile und Geländekanten. Dichte Vegetationsdecken und Überbauungen sind dabei stets ein Problem, da sie den direkten Blick auf die Bezugsoberfläche verhindern.
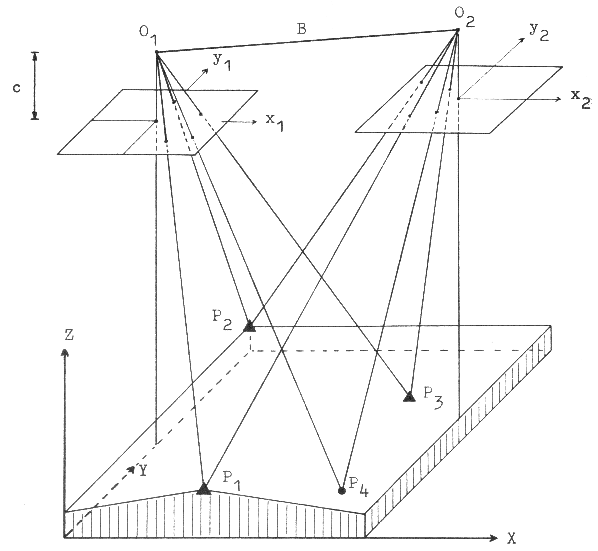
Für die Ermittlung des Z-Wertes wird jede Aufnahme eines Stereopaares orthometrisch durch Paßpunkte auf das tatsächliche Bezugsystem entzerrt und korregiert (Doppelbildeinschaltung 'räumlicher Vorwärtsschritt', vgl. Abb. 3.8.2). Aus den abweichenden, z.T. morphologieabhängigen Projektionsdaten bezüglich der gemeinsamen Paßpunkte im Gelände lassen sich nun die Bildkoordinaten in korrekte Landeskoordinaten (x, y,z) über Algorithmen (Details siehe z.B. Kraus, 1990) transformieren.
|
Abb. 3.8.2: Doppelbildeinschaltung mit Paßpunkten zur Ermittlung des Projektionsversatzes für die Orthoreferenzierung auf ein mögliches Landesbezugssystem (Kraus, 1990) |
In diesem vereinfachten Schritt wird das Landeskoordinatensystem über mathematische Beziehungen als dreidimensionales XYZ-System betrachtet, in dem das abgebildete Gelände in die xy-Ebene (Grundriß) und Höhe (z-Ebene) orthogonal projiziert wird. Tatsächliche Landeskoordinaten haben aber andere Bezugsflächen, die sich erheblich unterscheiden! So stehen die Höhen z.B. orthogonal zum Geoid, welches in erster mathematischer Näherung als Ellipsoid, in zweiter Näherung durch eine Kugel und erst in dritter Näherung durch eine Ebene ersetzt werden kann! Die Lagekoordinaten entstehen deshalb über ein komplexes mathematisches Abbildungsgleichungssystem des Erdellipsoides in die Ebene, wobei zwangsläufig Verzerrungen aufreten müssen, die jedoch klein gehalten werden können. Diese Fehler fließen bereits bei Maßstäben > 1:20.000 (Normalwinkel) in die dreidimensionale geometrische Auswertung ein. Um die Einflußnahme der Fehler zu minimieren müssen alle auszuwertenden Aufnahmen so genau wie möglich georeferenziert sein!
Digitale Zweibildauswertegeräte berücksichtigen in ihren Programmen derartige Fehler, wenn die digitalen Bildpaare bereits georeferenziert und auf das richtige Ellipsoid eingestellt sind. Bei der analytischen Auswertung werden dann über Meßmarken eines Quadratrasters (s.o.) in der xy-Ebene die Z-Werte ermittelt. So entsteht ein digitales Geländemodell auf Rasterbasis - dies kann auch über Anaglyphendarstellungen mit 3D-Einduck erfolgen (Abb. 3.8.3).
|
Abb. 3.8.3: Anaglyphenbild eines Häuserblocks im digitalen Ortho-Stereo-Luftbildpaar (cyan-rot-kodiert) |
|
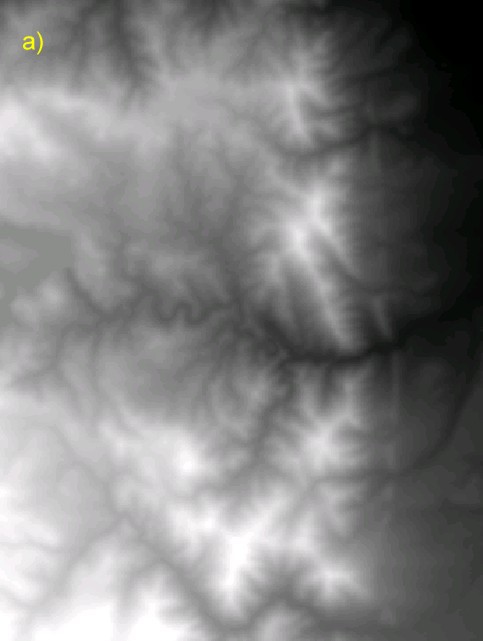
a) als Rasterbild höhenkodiert |
|
b) als perspektivisches DGM Abb. 3.8.4a und b: Digitales Höhendaten im Rastermodell (a) und als Oberflächen-DGM (b) |
DGM aus UAV/UAS Bildmosaiken (Stereoaufnahmen) oben
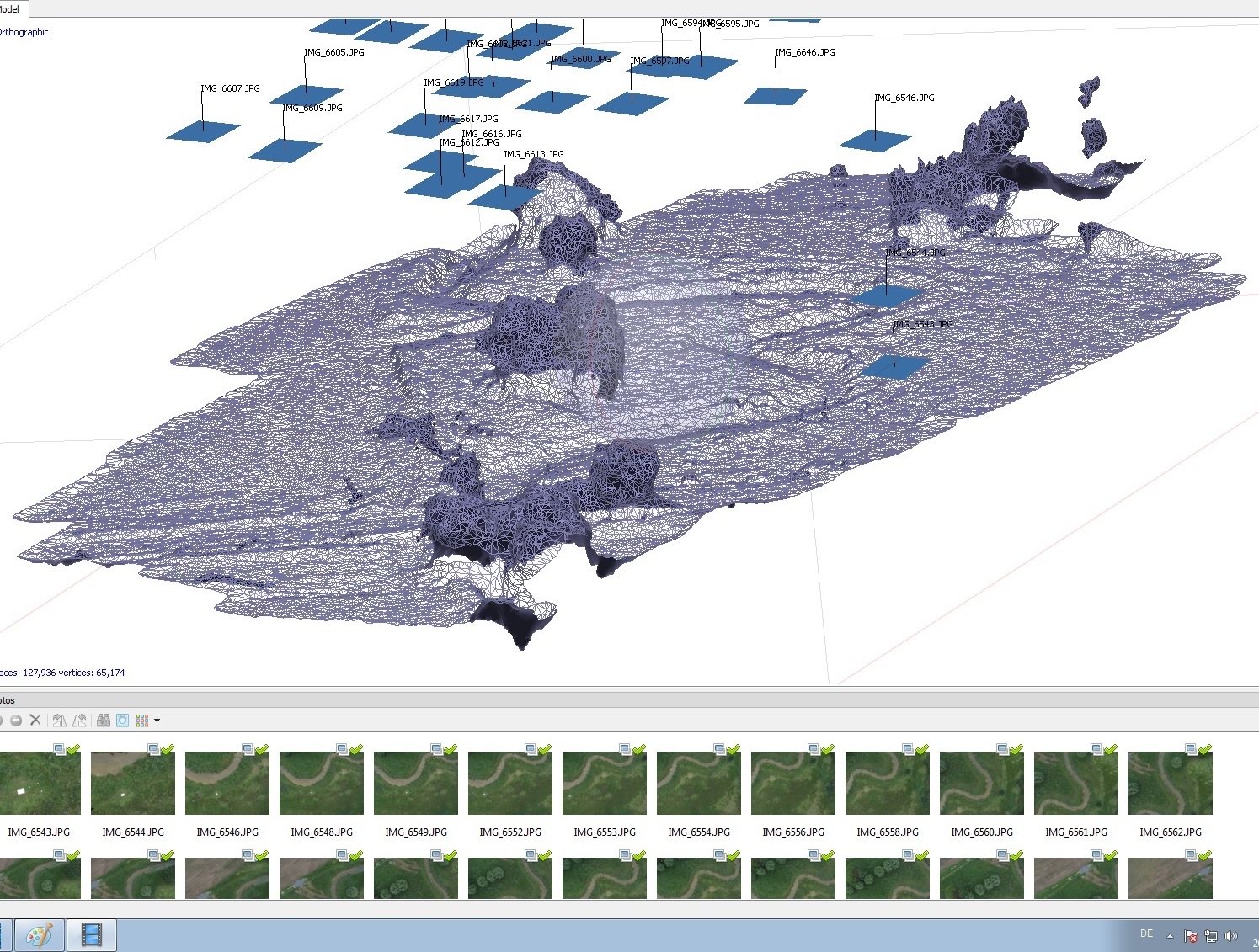
Eine methodisch innovative Form der Generierung von hochauflösenden, kleinräumigen DGM's ist die dreidimensionale digitale Analyse von UAV/UAS-Bildflügen (Dronenaufnahmen), verbunden mit der Ableitung von Punktwolken und Oberflächenmodellen (vgl. Abb. 3.8.5 bzw. 3.8.6).
In Anlehnung der klassischen Photogrammetrie können Programme wie Agisoft PhotoScan, OpenDroneMap (ODM) oder Pix4D aus hinreichend überlappenden Geländebildserien die räumliche Orientierung der Kamera (Projektionszentren) und der abgebildeten Geo-Objekte rekonstruieren bzw. berechnen.
|
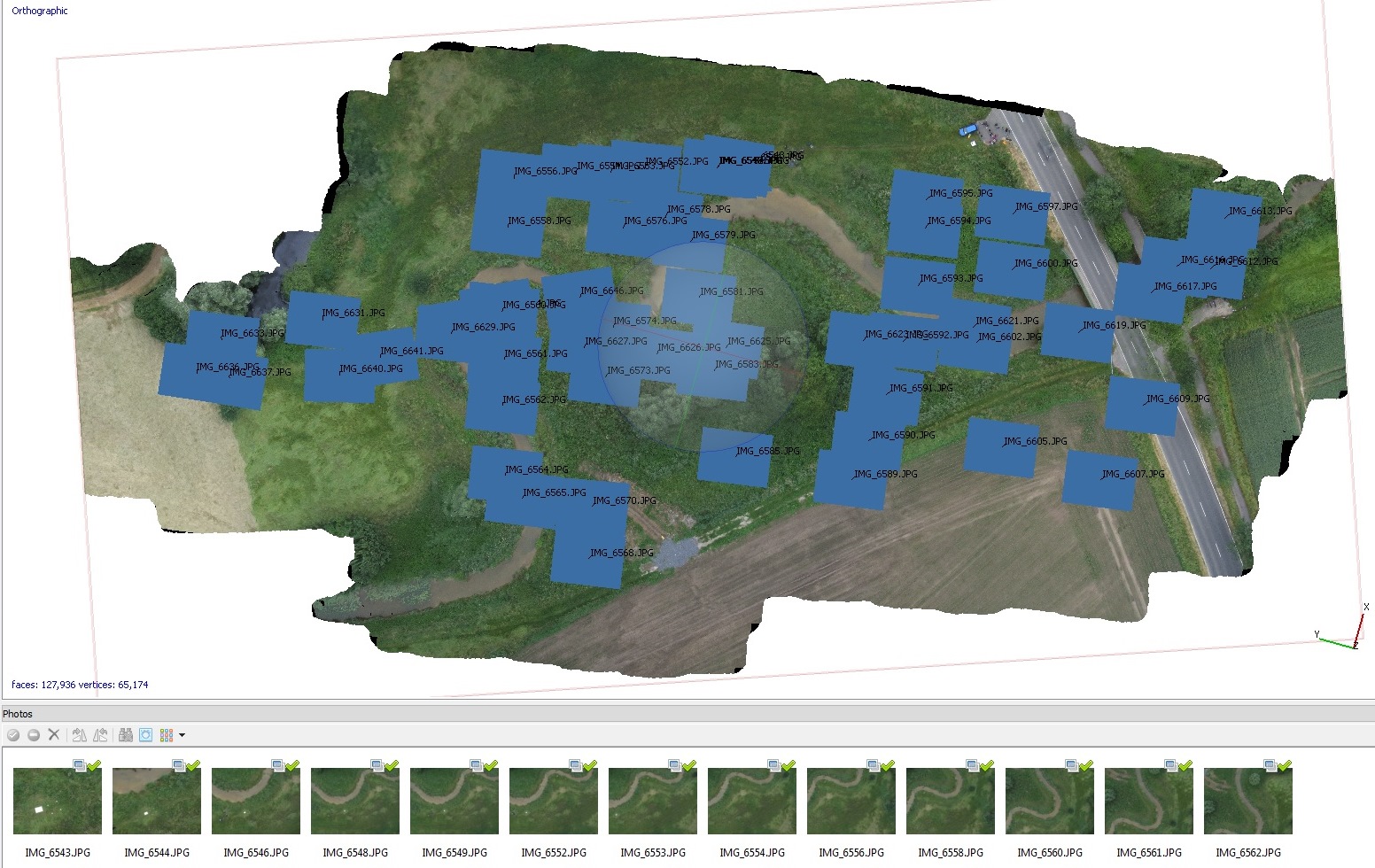
Abb. 3.8.5: Orthomosaik einer UAS-Befliegung der Aa nahe dem Zoo von Münster - viele Einzelbilder werden zu einem Mosaik mit rekonstruierten Projektionszentren automatisch zusammengefügt (Agisoft, IFGIcopter, 2015) |
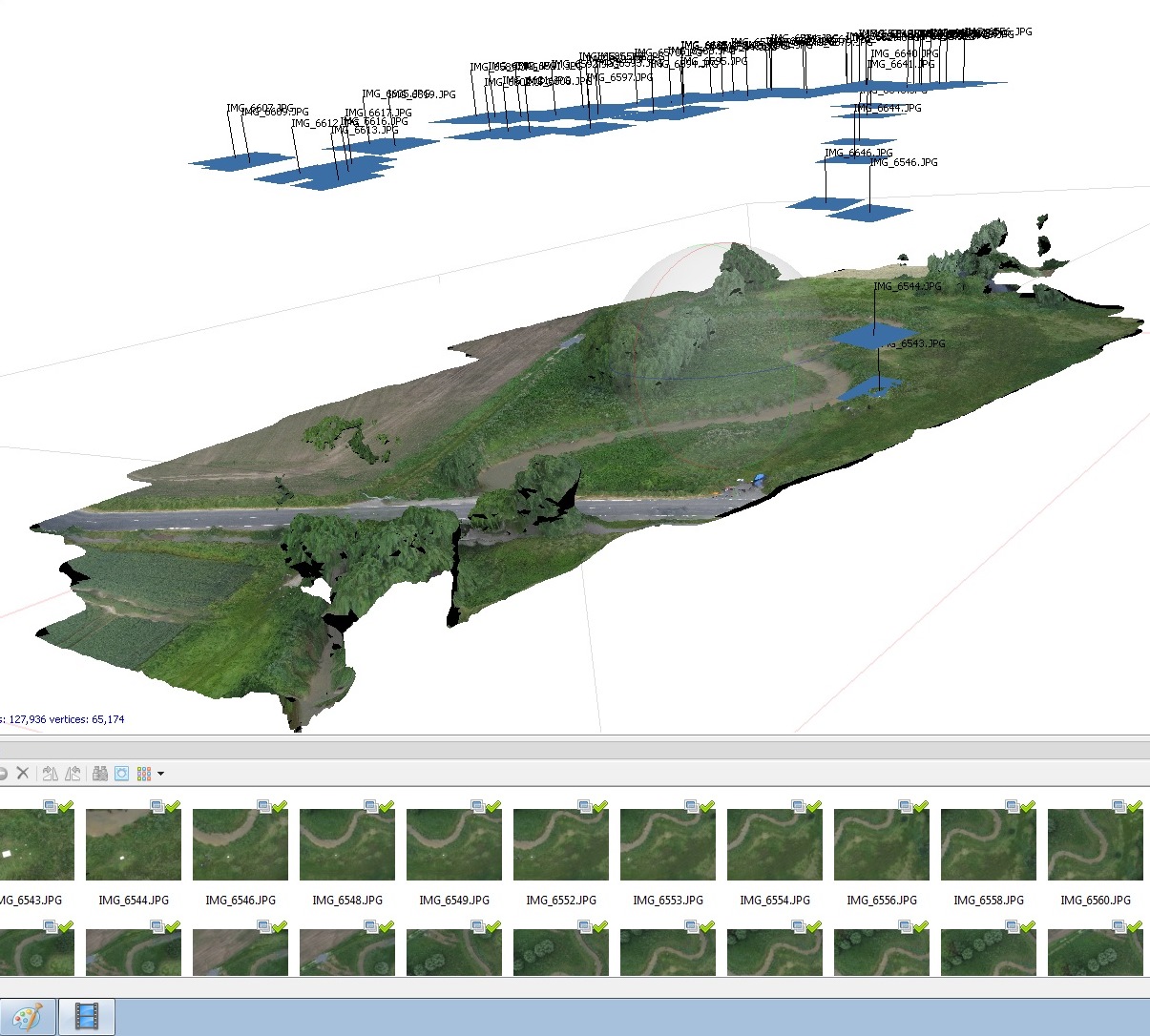
In diesen Punktwolken werden meist auch sein feiner Geländestrukturen, wie z.B. Gewässerlinien und einzelne, isoliert stehende topographische Punkte genau erfasst und stehen so bei der Interpretation bzw. virtuellen 3D-Animation zur Verfügung. Aus den verschiedenen Höhenmodellen können dann über Algorithmen auch rasterbasiertes DGM's erzeugt werden (vgl. Abb. 3.8.7) .
|
Abb. 3.8.6: 3D-Punktwolke des Untersuchungsraumes längs der Aa - auch kleine morphologische Unterschiede treten deutlich hervor (IFGIcopter, 2015) |
|
Abb. 3.8.7: Realtexturgefülltes, rasterbasiertes DGM aus UAS-Daten - die Layer werden zu einem virtuellen Geländemodell zusammengefügt (IFGIcopter, 2015) |
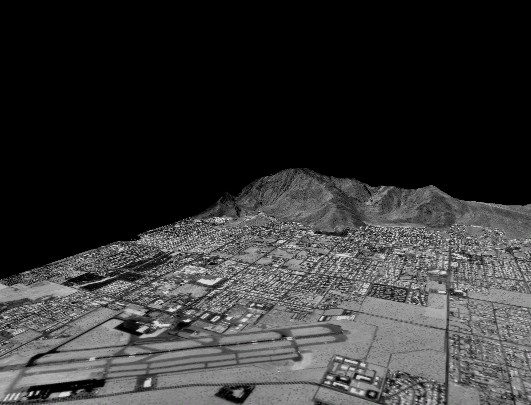
Der zeitliche Aufand einer derartigen Berechnung kann je nach Datenmenge und geometrischer Auflösung bis zu einigen Stunden dauern. Flächendeckende rasterbasierte DGM-Daten bzw. kommerziell vertriebene topographische 3D-Vektordaten sind somit i.d.R. recht kostspielig (Arbeits- und Zeitaufwand!). In Deutschland werden vergleichbare hochgenaue Produkte über die Landesvermessungsanstalten und -Ämter vertrieben. In den USA verfügt der USGS (US Geological Survey) über entsprechende DEM-Karten. Meist werden diese aber aus Radar- oder LIDAR-Daten (s.u.) abgeleitet.
|
Abb. 3.8.8: Rasterbasiertes DEM einer Region in der Wüste Nevadas mit virtueller, fiktiver Textur (USGS, 2002 ) |
DGM aus Laserscans oben
Airborne Laser Scanning ist eine moderne Methode zur direkten morphologischen Geländeaufnahme (vgl. Abb. 3.8.8a), die durch einen automatisierten Meßablauf (digitale Datenaufzeichnung und computerbasierte Auswertung) gekennzeichnet ist. In den letzten Jahren hat sich diese Technik aus dem prototypischen Stadium zu einem operationell einsetzbaren Verfahren entwickelt. Am bekanntesten in der Fernerkundung sind Oberflächenmessungen mittels LIDAR-Systemen (Light Detection And Ranging): Sie ist eine dem Radar (englisch radiowave detection and ranging) verwandte Methode zur optischen Abstands- und Geschwindigkeitsmessung sowie zur Fernmessung atmosphärischer Parameter. Statt Funkwellen wie beim Radar werden beim LIDAR Laserstrahlen verwendet..
Die Flugzeug-gestütze Laserscannermessung basiert auf einem Multisensorsystem mit den folgenden Komponenten:
- Laserdistanzmesser mit Scanvorrichtung
- DGPS-Empfänger
- Inertiales Navigationssystem (INS)
Ein Computer steuert die Einzelkomponenten und speichert die Daten zeitsynchron. Der Laserstrahl wird durch einen Spiegel quer zur Flugrichtung abgelenkt und die Laufzeit des ausgesendeten und von der Oberfläche reflektierten Signals gemessen (vgl.SAR-Verfahren/Mikrowellenstrahlung). Auf diese Weise wird ein Geländestreifen entlang des Flugweges abgetastet. Aus dem Abtastwinkel des Scanners und der Strahlungsfrequenz ergibt sich im Zusammenhang mit der Flughöhe über Grund, der Fluggeschwindigkeit und dem Abstand der Fluglinien die Dichte und Verteilung der Meßpunkte im Aufnahmegebiet.

Die Position und die Lage des Sensors im Raum werden aus den DGPS- bzw. INS-Messungen berechnet. Die Systemkalibrierung stützt sich auf Überlappungsbereiche zwischen einzelnen Streifen und Kontrollflächen mit möglichst geringer Oberflächenrauhigkeit (z.B. große versiegelte Parkplatzflächen). Die Kontrollflächen werden mit einem unabhängigen Verfahren (z.B. Tachymetrie) höhenmäßig erfasst. Insgesamt kann eine hohe Genauigkeit der Datenpunkte von < 1 cm in der Z-Komponente erreicht werden - die anfallenden Datenmengen sind jedoch sehr gross.
Resultierende Modelle bilden demnach feinste Unterschiede in der Morphologie ab (vgl. Abb. 3.8.8b). Über spezielle Filterverfahren lassen sich zudem auch unterschiedliche 'Vegetations-Horizonte' im 3D-Modell dedektieren (z.B. Blätterdach, Stammhöhe, humoser Untergrund etc.). Eine ausführliche Übersicht über grundlegende Airborne Laser Scanning Verfahren bietet Ackermann (1999 ff.).

DGM mit FE-Datenüberlagerung (Image Drape) oben
Für einige Analysen ist es wichtig, die digitale Bildinformation des FE-Datensatzes mit dem Geländemodell zu verschneiden (z.B. Landnutzung oder Erosionspotential in Abhängigkeit zur Morphodynamik eines Geländes). Um diesen aufwendigen Schritt vollziehen zu können bieten moderne Bildverarbeitungsprogramme ein sog. Image Drape (etwa 'Bildüberstülpung') an. Grundvoraussetzung ist ein gemeinsames Koordinatenbezugssystem von DGM und FE-Daten (Abb. 3.8.9).
|
Abb. 3.8.9: Rasterbasiertes DEM (a) und Luftbild-Daten (b) einer Region 'Palm Springs' (USA) im gemeinsamen UTM-System gemäß NAD 27 (ERDAS, 2005) |
Durch den Verschnitt der Daten werden virtuelle Landschaften erzeugt, die als Texturinformation die Grau- oder Farbwerte der FE-Daten tragen (Abb. 3.8.10). Landnutzungsinformationen bzw. physiogeographische Beschaffenheit des Untersuchungsraumes (z.B. Geologie, Böden, Drainage...) können somit geländegetreu abgebildet und interaktiv beeinflußt werden. Dies gilt auch für etwaige Klassifikationen oder geplante Eingriffe in den Raum (z.B. als Planungsgrundlagen).
|
Abb. 3.8.10: Image drape des Luftbildes über das DEM (ERDAS) |
Die Modifikation einer Darstellung von virtuellen Landschaften erfolgt in der Software durch Parameter wie Blickwinkel, Blickrichtung, Flughöhe, Zielpunkt, Sonnenstand, Strahlungsrichtung. (Abbildung 3.8.11) zeigt ein vergleichbares 3D Szenario, welches allerdings aus einem UAS-Bildmosaik mittels AGISOFT automatisiert als Anaglyphenbild (rot/grün-Brille!) erzeugt wurde.
|
Abb. 3.8.11: Anaglyphendarstellung des Landschaftsmodells ober Aa-Lauf bei MS, automatisch generiert mittels AGISOFT nach einem autonomen UAS-Bildmosaikflug (IFGIcopter, 2015) |
Für Präsentationszwecke werden zudem oft Animationen, wie 'Rundflüge' durch den Untersuchungsraum berechnet, um dem Betrachter einen Gesamteintdruck über das Gelände zu geben. Hierbei werden nicht nur FE-Daten mit dem DEM verschnitten, sondern auch Zusatzinformationen, welche morphodynamische Relevanz besitzen, in die Animation eingebunden. Typische Beispiele sind auch Einbindungen von 3D-image drapes in Viewer wie Google Earth oder Webportale (z.B. Klimawandel 17). Hier werden die meist aus Stereo-Ortholuftbildern extrahierten 3D-Informationen mit der Textur des jeweilgen (Gebäude-) Objektes zur Virtualisierung von Gebäudelandschaften herangezogen (vgl. Abb. 3.8.12 und Kap. 3.9).
Abb. 3.8.12: 3D-Gebäudekomplex des LWL Naturkundemuseums am Allwetterzoo Münster, abgeleitet aus einem Stereoluftbildpaar, visualisiert als KMZ-Datei in Google Earth (Photogrammetriekurs:.Demo-Bild anklicken *.kmz mit GoogleEarth zu öffnen!)
Ein Beispiel hybrider 3D-Einbindung sei im Hinblick auf die geologische Kartierung/Exploration des Pilgangoora Belts innerhalb der australischen Pilbara-Wüste (W.A.) gegeben...........