3.4 Farbsysteme

Die Erkennbarkeit von Objekten ist neben der geometrischen Form und dem Kontrast auch von ihrer spezifischen Farbgebung abhängig. Dies gilt natürlich nur für multispektrale, mehrkanalige Datensätze, obwohl sich einkanalige Fernerkundungsdaten auch in eine farbkodierte Form überführen lassen (dabei werden die als Maß der Reflexion skalierten Grauwerte gegen Farbwerte ausgetauscht). Im Folgenden beschäftigen wir uns nur mit der üblichen Farbgebung in digitalen, multispektralen Dreikanaldarstellungen von Geofernerkundungsdaten.

Farbtheorie und Definitionen
Der Begriff Farbe wird im allgemeinen für einen definierten 'Buntzustand' verwendet, wobei auch die gesamte Grauskala von Schwarz bis Weiß einbezogen wird (Kraus, 1990). Es ist wichtig hervorzuheben, daß es sich immer um Wahrnehmungen des menschlichen Sehorgans handelt, also um eine nicht eindeutige physikalische Größe! Das Empfinden einer Farbe kann von Mensch zu Mensch unterschiedlich oder gar gestört sein (z.B. 'Farbenblind').
Um jedoch für den technisch-praktischen Gebrauch die Vielfalt der Farben einordnen zu können, hat man verschiedene mathematische Farbsysteme entwickelt, die sowohl auf physiologischen als auch physikalischen Grundlagen basieren und somit dem menschlichen Farbempfinden qualitativ sowie qantitativ sehr nahekommen.

Digitale Farbbilder werden, um den Anforderungen der Farbsysteme gerecht zu werden,(Abb. 3.4.1) in Farbwertanteile (z.B. primäre Farben oder Grauwerte) zerlegt, die dann wiederum den einzelnen Farbkomponenten des Systems zugeordnet werden (colour coding). Von den unterschiedlichen Systemen sind insbesonders zwei Farbsysteme für die digitale Bildverarbeitung von Bedeutung:

- der RGB-Farbwürfel (orthogonales System)
- der IHS-Kegel bzw. -Zylinder (polares System)

Beide Systeme können problemlos ineinander überführt bzw. transformiert werden (RGB/IHS-Transformationen, s.u.).

RGB-Farbwürfel oben
Die Sehnerven des Menschen enden in der Netzhaut in Zäpfchen und Stäbchen, wobei die Zäpfchen für die Farbwahrnehmung zuständig sind. Die Empfindlichkeit der Rezeptoren liegt im Blau, Grün und Rot; alle anderen Farben entstehen durch Mischung dieser drei Farbanteile. Es ist deshalb für die Konzeption eines plausiblen Farbsystems naheliegend, diese drei Primärfarben als Koordinatenachsen in einem orthogonalen, dreidimensionalen, kartesischen System aufzunehmen.

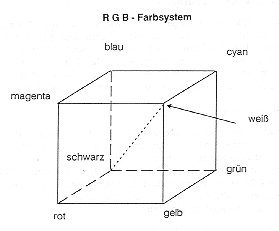
Als Koordinatenwerte werden die Intensität der jeweiligen Primärfarbe (0% = DN 0 bzw. 100% = DN 255, bei 8bit) an den Achsen abgetragen. Mischfarben ergeben sich in diesem additiven Farbwürfel durch eine Kombination der Einzelwerte R+G+B. Auf den nicht durch RGB besetzten Ecken des Farbwürfels sitzen die sogenannten Komplimentärfarben des subtraktiven Farbsystems auf (Cyan = Blaugrün, Magenta = Purpur und Yellow = Gelb). Diese komplimentären Farben liegen symmetrisch zum Würfelmittelpunkt (Abb. 3.4.2). Die Einheitsvektoren, die den Farbraum aufspannen werden auch als Primärvalenzen R,G,B bezeichnet.

Somit scheint die geometrische Form des Würfels als Grundlage sowohl für additive als auch subtraktive Farbmischungen geeignet. Im ersten Fall liegt der Nullpunkt bei Schwarz, im zweiten Fall bei Weiß. Sind die Farbwerte einer additiven Mischung gegeben, braucht man für die subtraktive Mischung nur das Komplement der Farbwerte auswählen und der Farbe die gegenüberliegende Würfelseite zuordnen.

Als Zahlenbeispiel soll eine Mischfarbe wie Braun über ihre jeweiligen Farbanteile berechnet werden:

- Additive Farbabschnitte R 40%; G 30%; B 10% ; daraus folgt
- Subtraktive Farbabschnitte C (100% - 40%), d.h. 60%; M (100% - 30%), d.h. 70%; Y (100% - 10%), d.h. 90%

Die Eigenschaften des Farbwürfels werden in der digitalen Bildverarbeitung einfach auf den Bildschirm übertragen. Jedes Pixel bekommt einen additiven Farbwert zugewiesen, der sich aus den drei Komponenten RGB zusammensetzt. Dies ist gleichzeitig der Grund dafür, daß Farbbilder eine ursprüngliche 24 bit-Farbtiefe aufweisen (3 x 8 bit). Die Farbintensität wird pro Kanal in 256 Stufen (= 8 bit) digital abgelegt und anschließend gemischt. Für die oben beschriebene Farbe Braun heißt dies:

- R = 255 x 0,4 = 102 (102 integer)
- G = 255 x 0,3 = 76,5 (76 integer)
- B = 255 x 0,1 = 25,5 (25 integer)

Für die Kombination von drei Kanälen bedeuted dies folglich, daß man zuerst den Reflexionsgrad eines jeden einzelnen Kanals in 256-stufige Intensitäten einteilt und jene dann wahlweise einem Einheitsvektor R, G oder B zugeteilt. Für jede Farbendarstellung ist es deshalb wichtig, neben den verwendeten Kanälen auch die gewählte Farbzuweisung (rgb) anzugeben (s.u. Falschfarbdarstellungen, Abb.3.4.3)!

IHS-Zylinder/Kegel oben
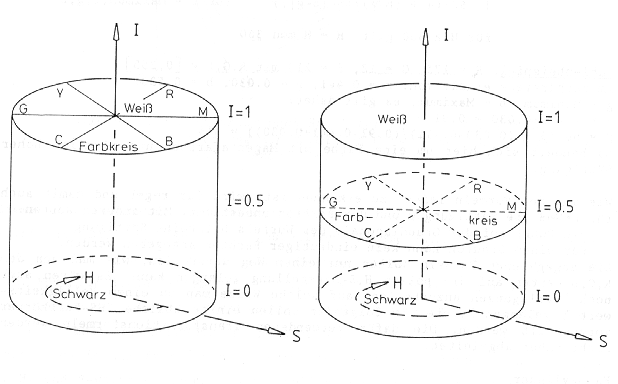
Als IHS-Systeme bezeichnet man all jene Farbsysteme, welche zur Charakterisierung einer Farbe die Begriffe Helligkeit (intensity, brightness), Farbton (hue) und Farbsättigung (saturation) heranziehen. Farbton und und -sättigung werden als polare Farbkoordinaten in einem Kreis (Winkel) abgetragen, dem der Helligkeitsfaktor als dritte Dimension hinzugefügt wird. Dies kann in Form eines Kegels oder eines Zylinders erfolgen (Abb. 3.4.4).

Die Intensität (I) verläuft immer in Z-Richtung, wobei I = 0 = Schwarz und I = 1 = Weiß ist; die Achse selbst repräsentiert den Grauwertvektor. Die Farbsättigung (S) wird als vektorielle Entfernung von der Kegel-/Zylinderachse/Graupfeil definiert, der Farbton (H) als Gradzahl im Farbkreis (über Rot, Magenta, Blau, Cyan, Grün und Gelb), d.h. es handelt sich um ein polares Koordinatensystem!

Die Verwendung des IHS-Systems ist mathematisch betrachtet eigentlich dem RGB-System an Präzision überlegen; in der digitalen Bildverarbeitung wird jedoch überwiegend das RGB-System bevorzugt, da es der menschlichen Wahrnehmung am nächsten kommt und weniger abstrakt ist.

Es ist zu beachten, daß IHS-Systeme nicht immer einheitlich definiert sind. Dasselbe gilt für die mathematischen Transformationsmethoden zwischen IHS- und RGB-Systemen! Bei der Definition des Farbtones kommt noch hinzu, daß Nullpunkt und Drehsinn beliebig angenommen werden können. Man kann daher IHS-Werte verschiedenen Ursprungs nicht ohne weiteres miteinander vergleichen.

Wichtig ist jedoch, daß ggf. feinste Spektralinformationen im IHS-System möglicherweise besser zum Ausdruck kommen, als dies im RGB-System der Fall wäre (allerdings werden andere Informationen auch stärker unterdrückt). Die IHS-Transformation ist jedoch besonders als mathematisches Bindeglied zur Verschneidung von unterschiedlichen geometrischen Auflösungen zweier FE-Datensätze von Bedeutung (vgl. resolution merge/pan-sharpening). Über die jeweils angewandte Transformationsformel informieren die mathemathischen Anhänge der Software-Produkte!

oben

nächstes Kapitel