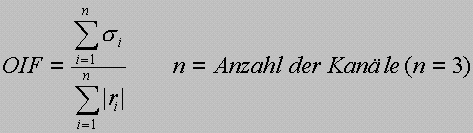3.2 Bildstatistik

Das Histogramm
Zur Grauwert-Charakteristik von Bildern gehören statistische Kennwerte, die bereits Aussagen über die Grauwertverteilung und damit über das zu erwartende Bild ermöglichen (Reflexionsgrad!). Üblicherweise wird in der digitalen Bildverarbeitung die Statistik der Bilder über ein Grauwert-Histogramm (Häufigkeitsvertweilung der DN-Werte!; DN = Digital Number) beschreiben (Abb. 3.2.1).

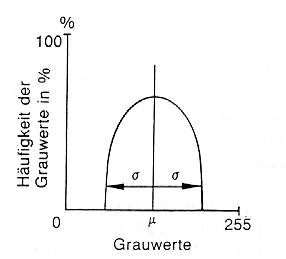Abb. 3.2.1: Histogramm eines digitalen Rasterbildes und deren grundlegende statistische Kenntwerte (aus Kappas, 1994)

Die wichtigsten grundlegenden statistischen Parameter sind hier:

- minimaler Grauwert (Gmin)
- maximaler Grauwert (Gmax)
- mittlerer Grauwert (Gmean)
- Standardabweichung ()
- Varianz ()

Minimaler und maximaler DN-Wert beschreiben den kleinsten und größten vorhandenen Grauwert und damit die maximale bzw. minimal gemessenen spektrale Reflexion/Helligkeit des Pixels. Der daraus abgeleitete mittleren Grauwert sagt zunächst etwas über die mittlere Gesamthelligkeit des Bildes aus. Liegt er nahe dem Wert Null (0 = schwarz) ist das Bild extrem dunkel; liegt er nahe dem Maximalwert 255 (= weiss) ist das Bild extrem hell (Abb. 3.2.2)!

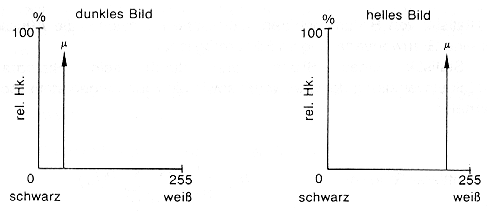Abb. 3.2.2: Lage der Mittelwerte von dunklen und hellen digitalen Rasterbildern (aus Kappas, 1994)

Die Standardabweichung und Varianz sagen etwas über den Kontrastumfang des Bildes aus. Ist die Standardabweichung groß, liegt ein kontrastreiches Bild vor (und umgekehrt!). Ähnliches gilt für die Varianz. Viel Kontrast bedeutet also, daß viele unterschiedliche Graustufen am Bildaufbau beteiligt sind und das Bild somit auch viel abgestufte Information enthält (Abb. 3.2.3). Ein kontrastarmes Bild ist durch eine geringe Streuung um den mittleren Grauwert gekennzeichnet; der Informationsgehalt ist deshalb oft geringer, da verhältnismäßig wenig verschiedene Grauwerte auftauchen (homogenes oder auch 'flaues' Bild). Kontrastarme Bilder werden grundsätzlich nachträglich einer geeigneten Kontraststreckung unterzogen (s.u.).

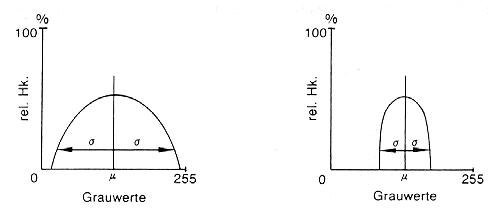Abb. 3.2.3: Histogramm eines digitalen Rasterbildes mit großem und geringem Kontrast (aus Kappas, 1994)

Einfache Bildverbesserung oben
Unter einfacher Bildverbesserung versteht man üblicherweise das Verbessern des Kontrastumfanges eines Datensatzes. Betrachtet man ein Histogramm eines Kanales (hier: TM-Scanner!) fällt auf, daß die Originalgrauwerte mehrheitlich niedrig und damit nicht gleichmäßig über das zur Verfügung stehende Grauwertspektrum von 256 Stufen verteilt sind. Eine Histogrammstreckung über lineare, ausgleichende oder wichtende Funktionen auf das gesamte Spektrum führt zu erheblichen Kontrastverbesserungen und damit zu einem enormen Informationsgewinn (Abb. 3.2.4; 3.2.5).

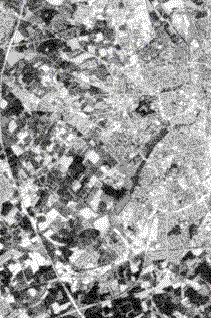Abb. 3.2.4: TM-Originalbild und linear gestreckes Bild von Münster (Kanal 3)

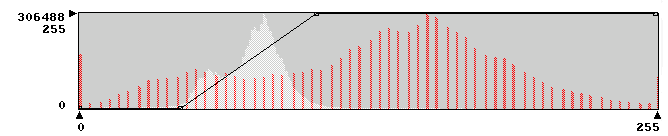Abb. 3.2.5: Histogramm des digitalen TM-Rasterbildes von Münster mit LUT-Funktion

Die Generierung des neuen, gestreckten Ausgabebildes wird über die Erstellung eines 'Look Up Tables' (LUT) erreicht, welche letztendlich der graphischen Darstellung (Abb. 3.2.6) einer mathematischen Transformationsfunktion entsprechen. Sinngemäß spricht man deshalb auch von einem 'LUT-strech' zur Hebung des Kontrastumfanges (Abb. 3.2.7).

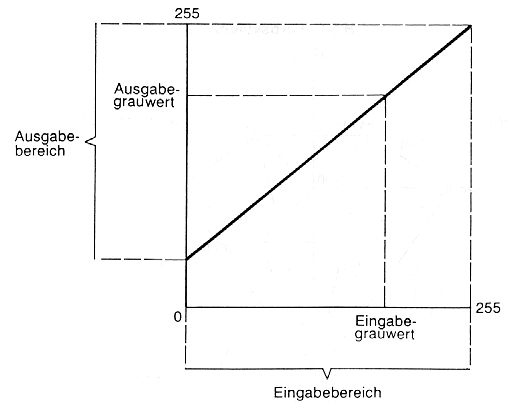Abb. 3.2.6: Ein-und Ausgabe-Raum eines digitalen Rasterbildes mit linearen LUT (aus Kappas, 1994)

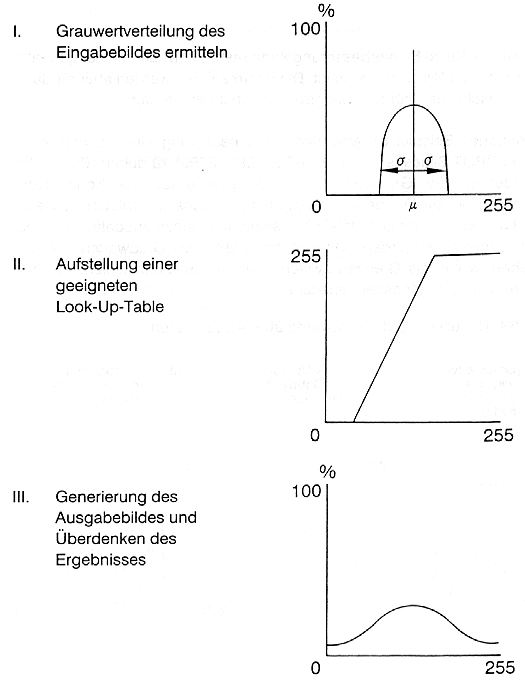Abb. 3.2.7: Vorgehensweise zur Histogramm-Streckung eines digitalen Rasterbildes mit linearen LUT (aus Kappas, 1994)

Obwohl die Definition der LUT-Streckung interaktiv modifiziert werden kann, sind in Bildverarbeitungsprogrammen wenigstens zwei Standardstreckungen als Angebot implementiert: Lineare LUT-Streckung und Histogramm-Ausgleichs-LUT-Streckung. Beide führen in ca. 80% der Fälle zu hinreichend guter Kontrastverbesserung.

Wichtig: Keine Bildverbesserung kann mehr Information erzeugen, als bereits im Bild vorhanden ist! Sie wird allerdings für das menschliche Auge transparenter!

Neben den oben beschriebenen Standardverfahren zur Kontrastverbesserung lassen sich LUT auch zur zielgesetzten Hervorhebung von Objektklassen benutzen. Ein einfaches Verfahren ist die Definition von Äquidensiten, welche vordefinierte Teile des Grauwertspektrums zu einzelnen Grauwertblöcken gleichen Wertes zusammenfassen (einfache Re-Klassifizierungen!), (Abb. 3.2.8). So lassen sich Grauwertklassen erzeugen, welche auch geowissenschaftlich, inhaltlich kohärent sind und einzelne Grauwertinformationen hervorheben bzw. unterdrücken (z.B. Gewässer DN 0-25, Waldflächen DN 30-40, Wolken DN 120-140, etc.).

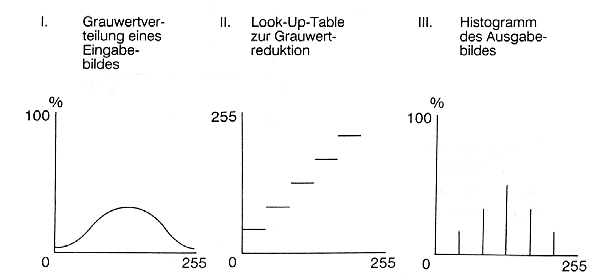Abb. 3.2.8: Ein-und Ausgabe-Histogramm eines digitalen Rasterbildes über Äquidensiten-LUT (aus Kappas, 1994)

Die obigen Histogrammdarstellungen gelten für einkanalige Bilddatensätze. Bei mehr Kanälen (multispektrale Daten) kommen zusätzlich weiterführende statistische Parameter hinsichtlich der Bildverbesserung zum Tragen.

Weiterführende statistische Parameter oben
Bei zwei- oder n-dimensionalen multispektralen Merkmalsräumen (jeder Kanal/jedes Spektrum entspricht einer Dimension!) erhält man als kombinierte Histogramme mehr oder minder elliptische DN-Punktwolken (Scattergramme), welche Informationen über den Korrelationsgrad (r) der Daten beinhalten.

Für die multispektrale Bildverarbeitung sind deshalb wichtig
- Korrelation (r)

und daraus ableitbar der
- Optimum-Index-Faktor (OIF)

(Zur Erinnerung: Zwei Datensätze sind stark miteinander korreliert, wenn die Ausgleichsgerade der Korrelationsfunktion die Steigung 1 oder -1 aufweist, d.h. völlige Korrelation = beide Datensätze sind gleich oder verhalten sich wie ein Negativ zum Positiv!. Ist r = 0, sind die beiden Datensätze unkorreliert; d.h. sie enthalten eine voneinander unabhängige Information)

Bereits die Form des zweidimensionalen Histogrammes gibt einen ersten Eindruck bzgl. der Korrelation von Datensätzen (Abb. 3.2.9). Ist die Ellipse schmal und gestreckt, so sind zwei Kanäle stark korreliert. Eine kreisförminge Grauwertverteilung weist auf sehr schwach korrelierte Kanäle hin. Für die multispektrale Auswertung von Satellitenbildern ist i.d.R. immer die Kombination von möglichst unkorrelierten Kanälen sinnvoll!

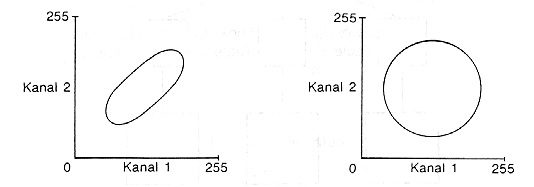Abb. 3.2.9: Zweidimensionales Histogramm zweikanaliger Rasterbilder und ihre Korrelation (aus Kappas, 1994)

Die Berechnung der Korrelation von multispektralen Datensätzen ist in den meisten Fernerkundungsprogrammen bereits implementiert, da diese statistischen Kennwerte u.a. auch für Klassifikationen genutzt werden (s.u.). Sie erfolgt meist über die Berechnung der Kovarianz (siehe auch Kappas, 1994) und führt zu einer Korrelationsmatrix, in der die Korrelationen der Kanäle untereinander ablesbar sind (Abb. 3.2.10).

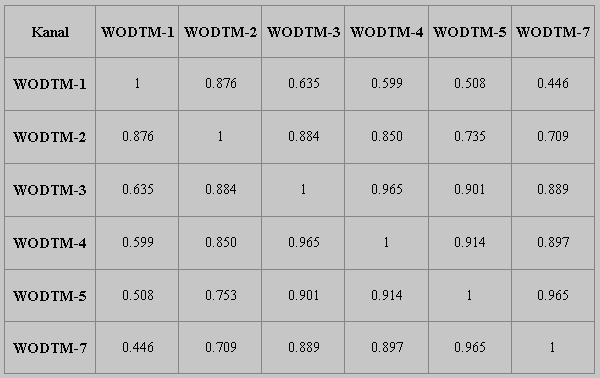Abb. 3.2.10: Beispiel einer Korrelationsmatrix (sechskanalige TM-Szene ohne emissives IR; aus Zumsprekel & Prinz, 1998)

Betrachtet man eine solche Korrelationsmatrix (hier: TM-Daten) fällt auf, daß die Kanäle innerhalb eines gemeinsamen, übergeordneten Spektrums (VIS oder IR) stark miteinander korrelieren. Kombinationen zwischen dem VIS- und dem IR-Spektrum zeigen jedoch geringere Korrelationen. Dies ist nicht verwunderlich, da viele Oberflächenmaterialien gerade im IR die deutlichsten Spektralunterschiede aufweisen und somit chrakteristischer abgebildet werden; die Differenzierbarkeit ist deshalb gerade hier sehr hoch! In multispektralen Falschfarbenbildern sollten somit Kombinationen aus Kanälen des sichtbaren Spektrums mit jenen des IR-Spektrums besonders hilfreich für die Ansprache von Geo-Objekten sein.

Optimum-Index-Faktor (OIF) oben
Um ein mathematisch objektives Auswahlkriterium für die optimale Farbkomposite zu ermitteln, läßt sich die Methode des Optimum-Index-Faktors (OIF) auf multispektrale Dreikanaldarstellungen anwenden (Prinz, 1996). Unter Berücksichtigung der Korrelation (r) sind generell Kombinationen geringer Redundanz in der weiteren Verarbeitung vorzuziehen (s.o.). Zusätzlich muß der Kontrastumfang (,) bewertet werden. Die mathematische Verknüpfung beider Faktoren für den OIF ist gegeben durch:

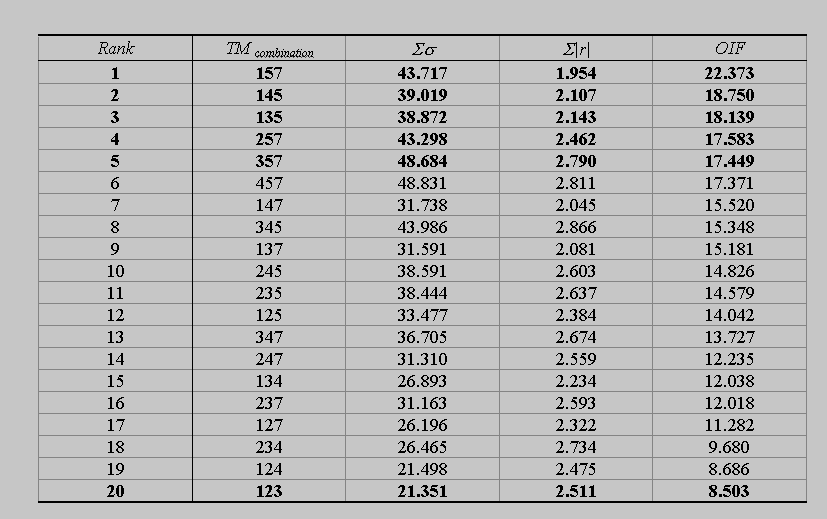
Je höher der OIF der ausfällt, desto mehr materialspezifische Unterschiede kommen spektral zur Ausprägung! Die Rangliste der informativsten Farbkompositen weist häufig eine Kombination aus zwei IR-Kanälen mit einem Kanals des VIS den höchsten spektralen Informationsgehalt zu. Es wird deutlich, daß eine Echtfarbendarstellung (TM-Kanäle 3, 2, 1 -> rgb!) für eine Interpretation statistisch ungeeignet erscheint (erfahrungsgemäß Platz 18 - 19!).

Die oben beschriebenen grundlegenden statistischen Methoden sind wichtige Werkzeuge um den Informationsgehalt eines (multispektralen) digitalen Bildes vorab zu berwerten und zu optimieren. Hierzu müßte im Extremfall das Bild nicht einmal visuell untersucht werden. Es ist jedoch immer möglich, dass genau die Information über ein spezielles Geo-Objekt während der allgemeinen Bildverbesserung verloren geht, auf das es die Interpreten besonders abgesehen haben. In diesem Fall müßen visuelle Kontrolle der Ergebnisdatensätze und evtl. komplexere mathematische Bildoperationen Verwendung finden!

Nach der statistischen Analyse und ersten Bildverbesserung sollten alle beteiligten Fernerkundungsdatensätze eines Projektes zunächst auf eine geographische Projektion rektifiziert werden, damit die internen geometrischen Verzerrungen minimiert und folgende Arbeitschritte im Hinblick auf alle Daten auf einer gemeinsamen geodätisch korrekten Bezugsebene durchführbar sind.

oben

nächstes Kapitel