
3.5 Spektraloperationen
Unter dem Begriff der Spektraloperationen sollen jene Bildoperationen zusammengefaßt werden, welche zur gezielten Herausarbeitung und Optimierung der Darstellung ausgewählter geowissenschaftlicher Bildinhalte dienen. Der zuvor bereits kennengelernte Prozeß der Grauwertstreckung (vgl. Kap. 3.2) ist i.w.S. auch eine Spektraloperation, wobei allerdings meist der allgemeine Charakter der Bildverbesserung dominiert (hier die Kontrastverbesserung).
Einfache arithmetische Pixeloperationen
Die Bildung von Datensummen, -quotienten (Ratios, Indices) oder Differenzen gehört zu den grundlegenden arithmetischen Pixeloperationen mit engerer Zielsetzung (z.B. change detection, LULC, monitoring). Dabei wird aus zwei oder mehreren Originaldatensätzen ein neuer, synthetischer Datensatz errechnet, der dann einen bestimmten Bildinhalt (z.B. Biomasse) focussiert wiedergibt (Abb. 3.5.1).
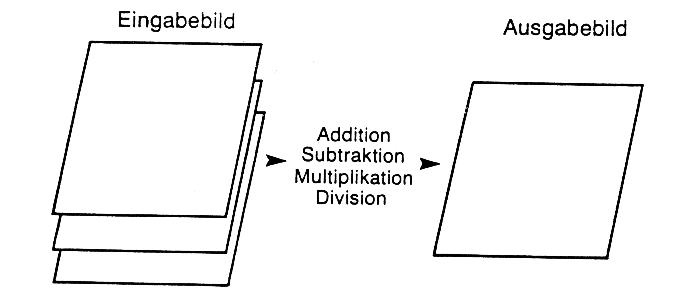 |
Abb. 3.5.1: Schematische Anwendung arithmetischer Operationen auf Rasterdaten (nach Kappas, 1994) |
Mathematischer Hintergrund derartiger Spektraloperationen (Raster-Algebra) ist die Tatsache, daß multispektrale Sensoren die variierenden Spektralcharakteristika von Oberflächenmaterialien in verschiedenen Kanälen numerisch aufnehmen und so Datensätze mit unterschiedlichen Grauwerten bzw. statistischem Charakter als Maß der unterschiedlichen Reflexion je Kanal vorliegen. Man vergleicht durch die arithmetische Funktion die Datensätze miteinander, in dem Wissen, daß sich bestimmte Zielobjekte in ihrer Spektralcharakteristik deutlich numerisch in den unterschiedlichen Kanälen voneinander abheben (z.B. eine möglichst geringe Redundanz der Grauwerte bzgl. einer Objektklasse besitzen!) und so im erechneten neuen Datensatz besser erkennbar sind. Materialspezifische (und deshalb häufiger verwendete) Operationen werden auch Indices geannt (z.B. Vegetationsindex).
Summen- und Differenzenbildung oben
Eine Mittelung oder Kompression der Information mehrerer Datensätze kann durch Summen- oder Differenzbildung erfolgen, wenn die unterschiedlichen Daten in ihrer Grauwertverteilung in etwa gleich sind (redundant). So wird die Addition oft zur Zusammenfassung ähnlicher Spektralbereiche zu einem panchromatischen Datensatz oder zur Kombination mit graphischen Rasterdaten (etwa Karten) genutzt. Eine spektrale Differenzbildung kann zu einem direkten Vergleich zweier Datensätze herangezogen werden. Nach der Durchführung beider Operationen werden die Daten i.d.R. in eine Integer-Zahl (ganze Zahlen) durch Streckung umgeformt. Dies erfolgt automatisch im 8bit-System von 0-255 DN. Weiterhin ist ein vorhergehender optischer Vergleich beider Ausgangshistogramme vor der Rechnung sinnvoll, da hier bereits über die mögliche Aussagefähigkeit des neuen Datensatzes geurteilt werden kann.
Sind zwei Histogramme nahezu gleichartig ( r = nahe 1 = höchste Redundanz!), können beide Kanäle addiert oder ein Kanal ganz verworfen werden, da er die gleiche Spektralinformation enthält. Eine Differenzbildung wäre nicht sinnvoll, da die resultierenden Werte gegen Null streben würden. Ähnlich unsinnig wäre eine Summenbildung gegensätzlicher Datensätze mit negativer Korrelation (Abb. 3.5.2), da hier eine flache DN-Verteilungen mit sehr wenig Kontrast resultieren würden.
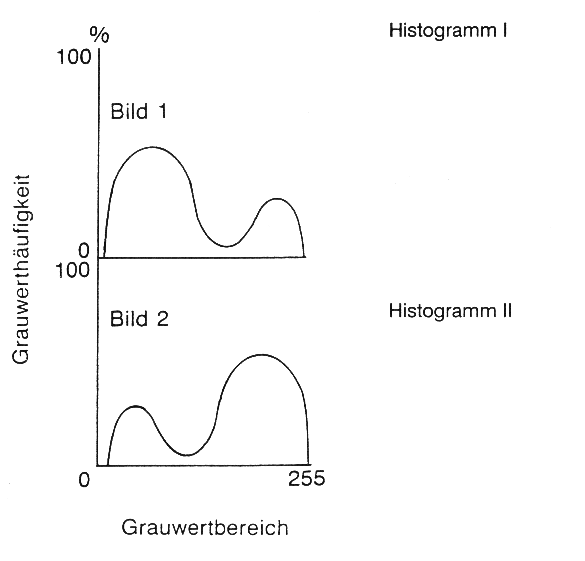 |
Abb. 3.5.2: Beispiel zweier Histogramme, mit denen eine Summenbildung wenig sinnvoll wäre; eine Verhältnisbildung (Ratio, s.u.) erscheint hier angebrachter (nach Kappas, 1994) |
Ratiobildung (Indizes) oben
Eine wesentlich wichtigere arithmetische Bildoperation ist die Quotienten- oder Verhältnisbildung von Datensätzen (Ratio/Indices). Die Ratiobildung ist ein bekanntes und teilweise standardisiertes Werkzeug der digitalen Aufbereitung (multispektraler) Datensätze, da hier sehr gezielt Spektraleigenschaften bestimmter Materialien (z.B. Vegetation, Minerale, Böden und Gesteine etc.) im neu errechneten Bild (sog. Index) hervorgehoben werden können. Dies gilt insbesondere für Materialien mit stark schwankenden Reflexionseigenschaften (bezogen auf den Verlauf des abgetasteten EMS/Kanäle). Durch die Ratiobildung werden also physikochemische Reflexions- und Absorptionsmaxima bzw. -minima der Oberflächenmaterialien miteinander in Verhältnis zueinander gesetzt.
Ein klassisches Beispiel ist die Vegetationsindizierung, welche bekanntlich im NIR die maximalen Reflexionswerte aufweist. Beispielhaft auf den LANDSAT TM Scanner bezogen heißt dies, daß in Kanal 4 die höchsten Grauwerte der Vegetation auftreten (Abb. 3.5.3), während in Kanal 2 (grün) oder 3 (rot) deutlich geringere DN-Werte gemessen werden. Vorausgesetzt, alle anderen Geo-Objekte weisen in diesen Kanälen eine mehr oder minder gleichmäßige Reflexionskurve auf (was streng genommen natürlich nicht immer der Fall ist), würde ein Ratio aus Kanal 4/3 besonders Areale mit gesunder Vegetation mittels hoher Grauwerte abbilden (Biomasse).
Derartige Ratios werden auch Vegetationsindex oder in seiner modifizierten Form Standardisierter/Normalisierter Differenz-Vegetationsindex (SDVI/NDVI) genannt.
Normalisierter Vegetationsindex = (TM 4 - TM 3) / (TM 4 + TM 3) = NDVI
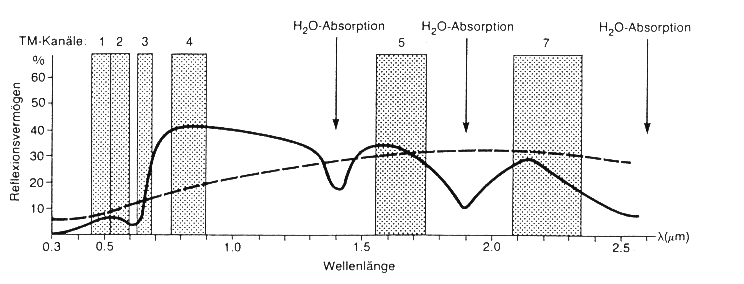 |
Abb. 3.5.3: Zusammenwirken von Summen-, Differenz- und Ratiobildung im Vegetationsindex bezogen auf LANDSAT TM-Kanäle für trockene Böden [---] und Vegetation [-] (nach Kappas, 1994) |
In der Pflanzenökologie ist (neben dem NDVI, siehe auch Abb. 3.5.4) auch ein weiterer Index wichtig, der z.B. bei Schädlingsbefall eine Reflexionsdifferenz von Totholzanteilen bzw. geschädigtem Blattwerk zu gesunder Laubdecke im IR aufzeigt. Es ist der sogenannte Normalized Difference Moisture oder auch Water Index (NDMI or NDWI, in Form der Landsat TM Spektral Kanäle 4 und 5 zu
Normalisierter Difference Moisture Index = (TM 4 - TM 5) / (TM 4 + TM 5) = NDMI
....this index contrasts the near-infrared (NIR) band 4, which is sensitive to the reflectance of leaf chlorophyll content to the mid-infrared (MIR) band 5, which is sensitive to the absorbance of leaf moisture......nach Goodwin et al. 2008).
Neben den oben beschriebenen Indices gibt es eine Vielzahl anderer, empirisch erprobter Ratios, welche wichtige natürliche Materialien in multispektralen Geofernerkundungsdaten charakterisieren können (hier beispielhaft für TM-Kanäle):
- einfacher Vegetationsindex TM 4 / TM 3
- grüner Vegetationsindex -0,29 x DN(TM 2) - 0,56 x DN(TM 3) + 0,60 x DN(TM 4) + 0,49 x DN(TM 4)
- Tonminerale TM 5 / TM 7
- Eisenminerale TM 5 / TM 4
- Eisenhydroxyde TM 5 / TM 3
- Eisenoxide TM 3 / TM 1
- Perpendicular Vegetation Index (PVI)......
Vgl. auch andere weiterführeden Literatur und und Software-Dokumentationen!
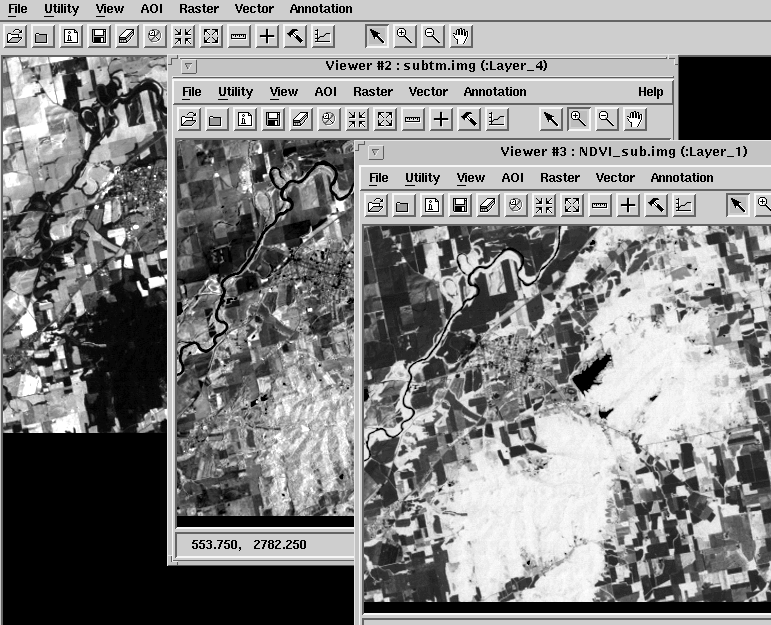 |
Abb. 3.5.4: Vergleich von TM-Daten zur Errechnung eines NDVI |
Auch für andere Materialien zeigt sich, daß generell Ratios von einem Kanal des VIS zu einem Kanal des IR für die Detektierung spezieller Geoobjekte wichtig sind - in besonderen Fälle auch Ratios aus NIR und Mid-IR Kanälen (z.B. Tonminerale). Diese Beobachtung läßt sich bereits indirekt aus dem geringeren Korrlelationsgrad der Datensätze und dem OIF ableiten (vgl. Kap. 3.1).
Einzelne Ratios werden anschließend oft zu hybriden Falschfarbenkompositen zusammengesetzt, die dann z.B. in Rottönen die Vegetation, in Grüntönen die Tonmineralgehalte und in Blautönen die Bodentypen differenzierbar visualisieren (TM 4/3; 5/7; 3/1 [rgb]).
Eine weitere Anwendung von Ratios besteht in der zeitlichen Betrachtung von Flächenveränderungen (Monitoring). Ziel kann so eine Verhältnisbildung zweier Kanäle aus unterschiedlichen Befliegungen sein, welche als Resultat die Bilanz der Veränderung über einen Zeitraum wieder gibt. Dieses Verfahren wird z.B. häufig zur Beurteilung von Brandschädigungen (Wald-oder Steppenbrand), aber auch von Abbau- bzw, Ernteprozessen oder Infrastrukturveränderungen genutzt (Abb. 3.4.5a,b,c).
Ein spezielles Ratio für den TM-Scanner wäre hier beispielhaft der Normalized Burn Ration (NBR):
((Landsat TM 4 - Landsat TM 5) / (Landsat TM 4 + Landsat TM 5)pre) - ((Landsat TM 4 - Landsat TM 5) / (Landsat TM 4 + Landsat TM 5)post)
Der NBR wird einzeln für ein Pre- und Post-Feuer Image gerechnet und voneinander subtrahiert. Er erlaubt so die flächenhafte Abschätzung der Schädigung bzw. Biomassenumwandlung (Klassifikation) und kann z.B. auch zur Analyse von Torfabbauflächen und deren Monitoring genutzt werden.

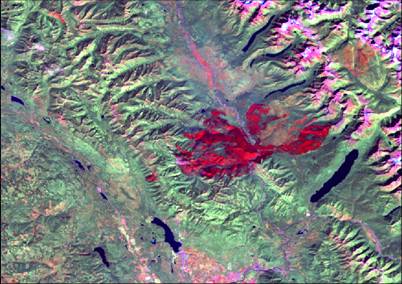
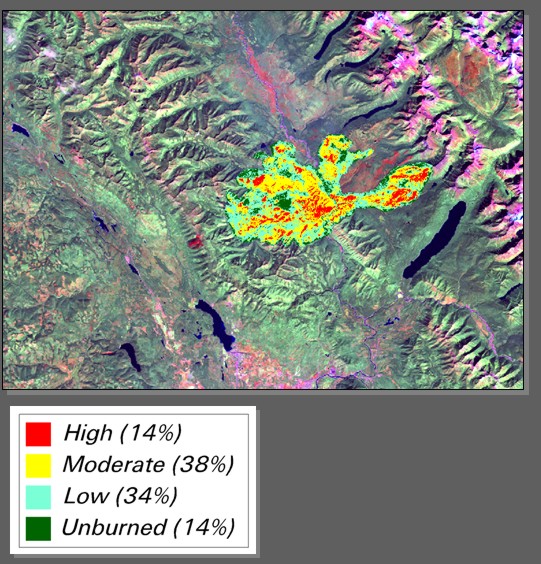
Abb. 3.4.5a, b,c): Vergleich des NBR von TM Daten als pre und post-burn image und als Bilanz
Auch topographische Effekte, wie Halbschatten oder teildiffuse Beleuchtungsverhältnisse werden in Ratios minimiert, da eine relative Angleichung der Grauwertverhältnisse erfolgt (Abb. 3.4.5 d)
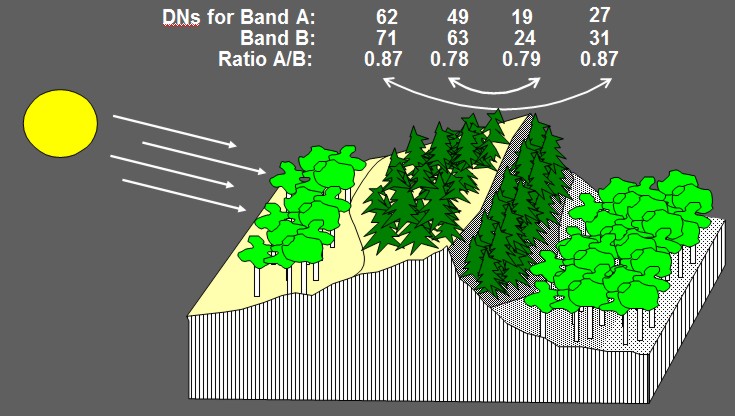
Abb. 3.4.5 d): Relative Angleichung verschiedener Beleuchtungseffekte durch Ratiobildung
Komplexe Pixeloperationen oben
Neben den oben beschriebenen relativ einfachen arithmetischen Pixeloperationen werden zur Herausarbeitung spezieller Bildinhalte auch wesentlich komplexere numerische Transformationen angewandt. Bereits bei der Summen-, Differenz- oder Ratiobildung muß man sich darüber im Klaren sein, daß mit den neuen, synthetischen Datensätzen in der späteren Bildanalyse nicht mehr auf originäre Spektralwerte zurückgegriffen wird. Dies gilt um so mehr für n-dimensional abgeleiteten Bilddaten wie z.B. Hauptkomponenten. Auch die RGB-IHS-(RGB-) Transformation gehört zur Gruppe der komplexen Pixeloperationen, genauso wie unterschiedliche Filteroperationen und die Tasseled Cap Analyse!
Hauptkomponenten-Transformation/-Analyse oben
Die Hauptkomponenten- oder auch Kahunen-Loeve-Transformation/ -analyse (engl.: principal component analysis = PCA) ist ein statistisch aufwendigeres Verfahren, welches besonders dann Anwendung findet, wenn die originären Grauwerte eines Multispektralbildes innerhalb der Spektralkanäle sehr stark korrelieren. Ihre theoretisch-mathematische Ableitung soll an dieser Stelle nicht im Detail ausgeführt werden und kann bei Haberäcker (1987) oder Kraus (1990) nachvollzogen werden. Hier sollen nur die wesentlichen Züge der Transformation und die Charakteristika der Hauptkomponenten skizziert werden:
Obwohl mit der Errechnung des OIF's bereits ein gutes Werkzeug zur Definition geeigneter Falschfarbenkompositen besteht, kommt es dennoch oft vor, daß die Grauwerte der Originalkanäle auch multispektral stark korrelieren bzw. nur unzureichend im Hinblick einer Objektdifferenzierung unterscheiden. Um diese Korrelation zu überwinden und die wellenlängenabhängigen materialspezifischen Spektralunterschiede zu verstärken wird eine Hauptkomponenten-Transformation der jeweiligen Grauwerte durchgeführt. Die Transformation erlaubt so die Berechnung neuer, synthetischer Datensätze, welche nur die unkorrelierten Spektralunterschiede abbilden (Donker & Mulder, 1976). Wichtig ist hier die Verstärkung und Darstellung der voneinander unabhängigen Spektralinformationen in Datensätzen höherer, bzw. auch n-dimensionaler Ordnung.
Im Folgenden soll kurz die Wirkungsweise einer zweidimensionalen PCA (oder auch HKA) skizziert werden (Abb.3.5.5).
Die Transformation der voneinander abhängigen Grauwerte DN(k) in neue, unabhängige Grauwerte DN*(k) erfolgt über die Definition eines (hier vereinfachend) zweidimensionalen Merkmalsraumes (bei eine vollständigen Transformation besitzt der Merkmalsraum soviele Dimensionen wie Kanäle, d.h. bei TM also 6 Dimensionen, entsprechend der 6 reflektiven Bänder!).
Die Grauwertverteilung zeigt allg. eine elliptische Form und belegt so den hohen Korrelationsgrad der Reflexionswerte (Abb. 3.5.5a). Zunächst versetzt (translatiert) die PCA den Ursprung des Achsensystems an den Punkt, an dem die Mittelwerte mx und my der beiden Datensätze gemeinsam definiert sind (Abb. 3.5.5b). Anschließend werden die Achsen um einen Winkel u gedreht, so daß eine Achse entlang der größten Varianz der Daten ausgerichtet ist (Abb. 3.5.5c). Selbige Achse bildet vektoriell die erste Hauptkomponente (HK-1) und repräsentiert die größten unkorrelierten Spektralunterschiede; die senkrecht zu ihr stehende Achse wird als zweite HK bezeichnet und repräsentiert einen ebenfalls einen Vektor (Transformation des Zahlenraumes!).
Hervorgerufen wird diese Drehung der Achsen durch eine Transformationsmatrix, welche lediglich auf die Eigenwerte der Vektoren und die Varianz-/Kovarianzmatrix der beteiligten Datensätze zurückgreift. Bei mehr als zwei Dimensionen resultieren folglich auch n-dimensionale Ellipsoide mit entsprechender Anzahl von Raumachsen. Die Größe der Hauptkomponenten wird als skalarer Wert (Vektor) abgebildet. Um die skalaren Größen dann wieder in Form von Grauwerten darstellen zu können erfolgt eine Retransformation in den urpsrünglichen Raum ganzer Zahlen (DN-values!).
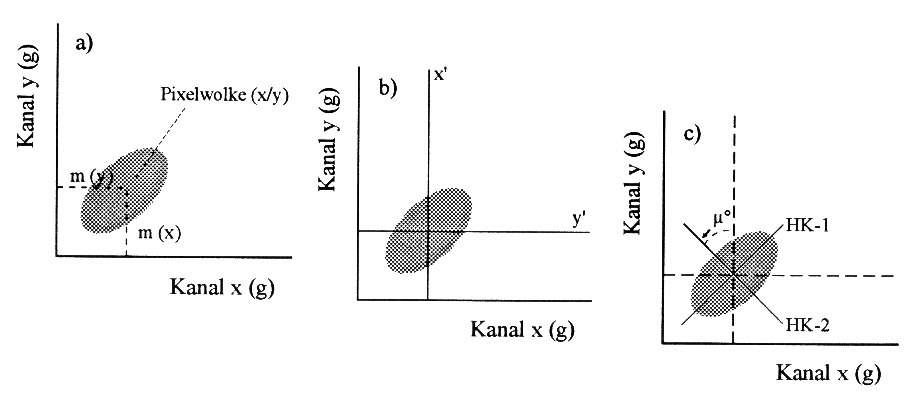 |
Abb. 3.5.5: Prinzip einer zweidimen- sionalen Hauptkompo- nenten- Transform- ation (aus Prinz, 1995) |
Aus den neu errechneten HK's werden nun diejenigen nach Größe sortiert ausgewählt, welche die größten Standardabweichungen bzw. größten Eigenwerte (eigenvalues) besitzen.
Auf diese Weise wird die redundante Information durch eine Linearoperation auf eine geringere Anzahl von Kanälen komprimiert (allg. repräsentiert die 1.HK ein systemunabhängiges Abbild der Gesamtalbedo, die 2.HK die z.B. systemabhängigen Albedounterschiede zwischen VIS und IR-Spektrum, die 3.HK systemabhängige interne Albedounterschiede innerhalb des IR oder des VIS, höhere HK's individuelle Unterschiede wie z.B. temporäres Rauschen [engl.: noise]). Mit steigendem Ordnungsgrad der HK dominiert zunehmend das elektronische Rauschen der Datenübertragung (also immer geringere unkorrelierte Unterschiede zwischen den Kanälen, meist ohne jeglichen Geo-Bezug).
Erfahrungsgemäß stellen die ersten drei bis vier HK's eine gute Grundlage zur Interpretation von geowissenschaftlichen Merkmalen im Bild dar (Grunicke, 1990; Prinz & Bischoff, 1995).
In Abbildung 3.5.6 sind die sechs HK's einer TM-Szene wiedergegeben; man beachte die abnehmende Bildqualität aufgrund der immer geringer werdenden dekorrelierten Unterschiede in den DN-Werten mit höherer HK-Ordnung!
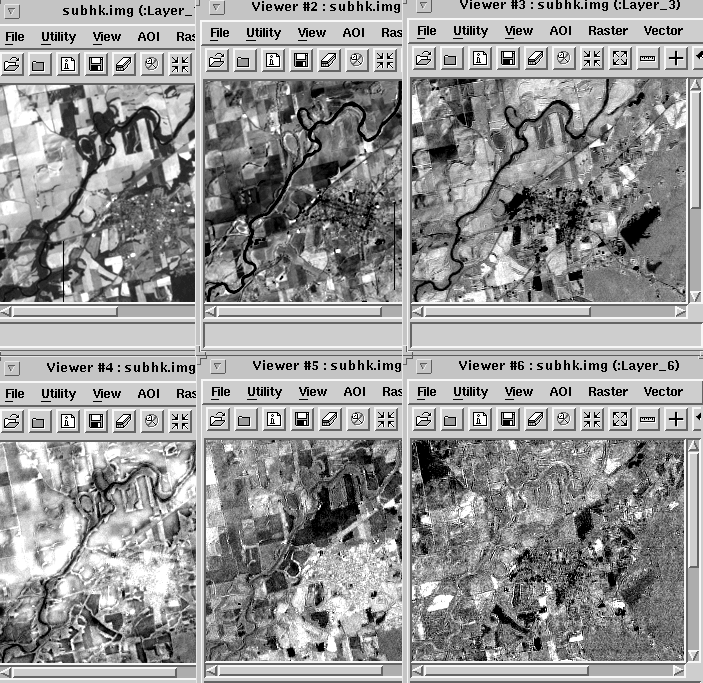 |
Abb. 3.5.6: Die sechs Haupt- komponenten eines TM- Datensatzes |
Hauptkomponenten werden auch zu Falschfarbenkompositen zusammengefaßt (Abb. 3.5.7). Eine HKA kann auch bewußt für eine begrenzte Anzahl von Kanälen durchgeführt werden, wenn es z.B. darum geht, nur die Gesamtalbedo des VIS oder des IR Spektrums zusammenzufassen. Solche Einzelkomponenten werden dann gezielt mit anderen Originalkanälen oder Ratios zu hybriden Falschfarbkompositen zusammengefügt.
Merke: Bei der Differenzierung von Geo-Objekten sollte man sich immer darüber im Klaren sein, daß die Farbgebung der Objekte nicht mehr durch die originären Reflexionswerte verursacht wird, sondern vielmehr ein statistisches Maß der weitgehend unkorrelierte Spektralunterschiede unterschiedlichster Ordnung durch Farbvektoren im RGB-Bildraum ist (folglich einen sehr hohen Abstraktionsgrad bzgl. der Information besitzt!). Hauptkomponenten können natürlich auch für jede Art der Rasterdaten berechnet werden, also auch für Ratios, Summen usw..
 |
Abb. 3.5.7: Die ersten drei Hauptkomponenten des TM-Datensatzes von Louisville als Falschfarbenkomposite HK 3; 2; 1 [rgb] |
Tasseled Cap Transformation oben
Das Tasseled Cap (etwa 'Zipfel- oder Fransen-Mütze') Verfahren/Transformation in der Fernerkundung stellt die Umformung der Albedowerte eines multispektralen Datensatzes in Einzelkompositen mit bestimmter thematischer, meist vegetationsfocussierender Ausrichtung dar; dies bedeuted i.d.R. die gewichteten Summen verschiedener Kanäle und deren Grauwerte im Hinblick auf einen speziellen Objekttyp. Das Verfahren wurde 1976 von R.J. Kauth and G.S. Thomas am Environmental Research Institute of Michigan in einem Artikel "The tasseled Cap -- A Graphic Description of the Spectral-Temporal Development of Agricultural Crops as Seen by LANDSAT" erstmals beschrieben. In diesem Artikel zeigen Kauth und Thomas die Verknüpfung typischer Albedo-Muster in LANDSAT MSS-Daten im Hinblick auf die zyklische Vitalität von Feldfrüchten mittels gewichteter Summenbildungen auf.
Einer dieser gewichteten Summen ist die Helligkeit (Brightness) eines jeden Pixels in der Aufnahme (in Abhängigkeit zur zeitlich variierenden Reife einer Pflanze). Die anderen Kompositenwerte sind meist Linearkombinationen aus Werten aller anderen beteiligter Kanäle, manche mit positiver, anderen mit negativer Gewichtung. Einer dieser anderen wichtigen Komponenten ist der sogenannte 'Grünfaktor' oder auch Greenness der Pixel (Vitalität i.w.S.); andere können unter Umständen den Gelbanteil (Yellowness) der Vegetation (Reife i.w.S.) beschreiben oder auch die Feuchte des Bodens. Eine ggf. auftretende Restalbedo wird als 'Sonstiges' (other)' berschrieben. Überlicherweise verwendet man nur drei TC-Kompositen Brightness, Greeness, Yellowness für die Berechnung/Analyse.
Der Erfolg des Tasseled Cap Verfahrens kann auch empirisch im direkten Vergleich zur Wirklichkeit (Ground Truth) belegt werden. Das methodische Vorgehen ist stark an die Hauptkomponenten Transformation angelehnt und wurde von ihr inspiriert. Auch die HKA (s.o.) bedient sich gewichteter Variablen (Eigenvektoren) aus gewichteten Summen von Einzelkanälen. Typischerweise enthalten die ersten Komponenten die Hauptinformation bzgl. Landsat MSS oder TM Daten - die HKA führt also zu einer Reduktion und Kompression der multispektralen Information. So bildet die 1. HK z.B. immer die Gesamtalbedo aller Kanäle ab (vgl. Brightness bei TC!).
Die Tasseled Cap Transformation korrespondiert also in gewisser Weise mit der HKA, insofern sie die Datensätze auch einem neuen orthogonalen Koordinatensystem anpasst. Sie bedient sich hier aber einer Generalisierung aufgrund von empirischen Feldbeobachtungen, wobei die mathematischen Ansätze naturgemäß analytisch sind.
Das Prinzip (vgl. Abb. 3.5.7a): Die Charakteristika für vegetationsfreie helle oder dunkle Böden sind stark variierend, da die Albedo neben der Zusammensetzung des Bodens z.B. auch von dem Beleuchtungswinkel, Sonnenstand, Hangneigung abhängig ist (in Abb. 3.5.7a die soil values A1 und B1 fallen in eine Linie durch den Ursprung, sind also mit 1 korreliert). Dies Korrlelation wird zunehmend aufgehoben, wenn erstmalig Vegetation auftritt und zunehmend heranreift (vgl. auch Kauth & Thomas, 1976):
....in a real wheat field there will be a distribution of the readings for bare soil along a ellipsoid as a result of variations in soil types and land angle relative to the sun angle. With growing wheat there will be variation among the wheat plants as to the stage in the life cycle. Thus the plot of the data for a wheat field may resemble a cap as shown in the diagram below ....
.....as a crop such as wheat emerges from dark soil there is an increase in reflectance in the near IR band because of the reflectance of chlorophyll but a decrease in the red band because of chlorophyll's absorption of red light. Also the plants create shadows that result in lower readings from the soil. The shadowing of the soil by the plants will depend upon the orientation of the crop rows compared to the angle of the sun. If the sun is shining down the rows the shadows on the soil will be less that if the crop rows are prependicular to the direction of the sun.
The net result is that as the wheat plants grow the near IR readings have a net gain and the red readings have a net loss as shown by the points A2 and A3 in the diagram below. For light soils the pattern may be different. The light soil has a high enough reflectance that as the wheat plants grows the reflectance of the plant even in the near IR band is not enough replace the loss of reflectance from the light soil so readings decrease in both bands but more so in the red band than in the near IR band.... This is shown by points B2 and B3 ...... (Kauth and Thomas,1976)
Dieser Zusammenhang wird in Abb. 3.5.7a bzw. b wie folgt wiedergegeben:
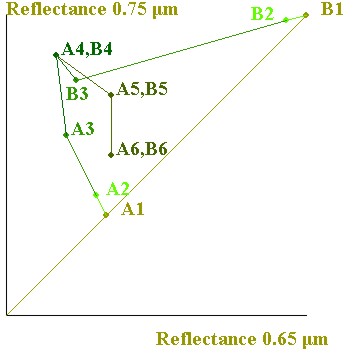 |
Abb. 3.5.7a: Zweidimensionaler Merkmalsraum mit typischen Albedowerten für normale, dunklere (A1) und hellere Böden (B1) und Vegetation unterschiedlicher Reife, die zur Form einer Tasseled Cap führen (dunkle Böden A2, A3 bzw. helle Böden B2, B3). A4 und B4 geschlossene Vegetationsdecke beider Böden. Zunehmende Reife (Yellowness!) A5/B5 bis A6/B6. |
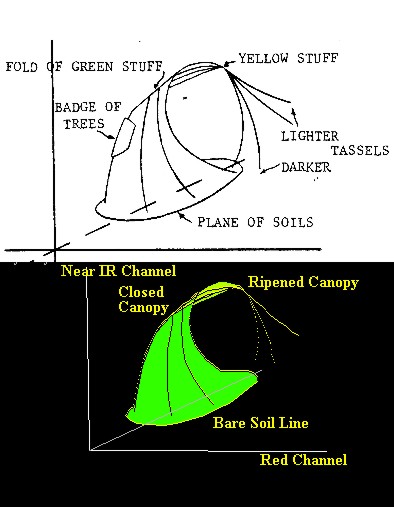 |
Abb. 3.5.7b: Dreidimensionaler Merkmalsraum mit typischen Albedowerten für unterschiedlich helle Böden und Vegetation unterschiedlicher Reife einer Tasseled Cap als empirische 3D Grenzflächen |
Wenn die Vegetationsdecke heranreift schliessen sich langsam die lichtdurchlässigen Lücken über dem Boden und als Effekt wandert die Reflektion der dunklen und hellen Böden zum Punkt A4 und B4, also zum NIR. Von dort an sind die Reflektionswerte ähnlich für beide Boden-Typen, da diese zunehmend vegetationsbedeckt sind. Mit voranschreitender Reife verändert sich die Albedo der Feldfrüchte hin zu mehr Gelbanteilen, wie in A5 und B5. Bei völliger Reife fällt die Reflektion drastisch im NIR ab (Trockenheit in A6 und B6).
Das Verfahren nach Kauth und Thomas basiert auf dem empirischen Vergleich von Testgebieten und der Form der jeweiligen 'Kappe' (Cap). Eine Komponente ist die gewichtete Summe der Albedo (brightness). Die zweite Komponente steht rechtwinklig zur Ersten und seine Achse verläuft durch den Punkt der 'zunehmender Vegetationsreife', korrespondierend zu Punkt A4 und B4. Die dritte Komponente korrespondiert zu einer weiteren Achse, rechtwinklig zur Ersten und Zweiten und verläuft durch den Punkt der absoluten Reife (yellow stuff). Eine vierte Komponente repräsentiert das 'Restrauschen' (sonstige). Für Landsat MSS bedeuted dies:
| GEWICHTUNG FÜR TASSELED CAP TRANSFORMATIONEN VON LANDSAT MSS DATEN |
||||
|---|---|---|---|---|
| Komponenten | Kanal 1 | Kanal 2 | Kanal 3 | Kanal 4 |
| Brightness | 0.433 | 0.632 | 0.586 | 0.264 |
| Greenness | -0.290 | -0.562 | 0.600 | 0.491 |
| Yellowness | -0.829 | 0.522 | -0.039 | 0.194 |
| "sonstige" | 0.223 | 0.012 | -0.543 | 0.810 |
Die Wichtung der ersten Komponente wurden anhand von Analysen von MSS Daten im Fayette County, Illinois ermittelt. Der 'Grünpunkt' basiert dort auf einem Maisfeld-Muster. Kauth und Thomas hatten keine Möglichkeit einen 'Gelbpunkt' direkt quantitativ zu messen, orientierten sich deshalb an einer gelblichen Mais-Variante um sich diesem spektralen Charakteristikum anzunähern.
Crist und Cicone (1984) adaptierten das Tasseled Cap Verfahren für die sechs reflektiven Kanäle des moderneren Thematic Mapper (TM). Die Gewichtung ist ein wenig anders als bei MSS Daten; insbesondere die dritte Komponente wird als repräsentativ für die Bodenfeuchte gesehen, also etwas anderes als bei Kauth und Thomas:
| GEWICHTUNG FÜR TASSELED CAP TRANSFORMATIONEN VON THEMATIC MAPPER DATEN |
||||||
|---|---|---|---|---|---|---|
| Komponente | Kanal 1 | Kanal 2 | Kanal 3 | Kanal 4 | Kanal 5 | Kanal 7 |
| Brightness | 0.3037 | 0.2793 | 0.4343 | 0.5585 | 0.5082 | 0.1863 |
| Greenness | -0.2848 | -0.2435 | -0.5436 | 0.7243 | 0.0840 | -0.1800 |
| Wetness | 0.1509 | 0.1793 | 0.3299 | 0.3406 | -0.7112 | -0.4572 |
Praktisch heisst dies für TM-Daten, dass im Algorithmus sechs von sieben möglichen Landsat TM Bänder genutzt werden, wobei 3 Informationsebenen zusammengefasst (transformiert) erscheinen:
- Tasseled Cap 1 (brightness, ein Messwert für den Boden)
- Tasseled Cap 2 (greeness, ein Messwert für die Vegetation)
- Tasseled Cap 3 (wetness, ein Messwert für Interaktionen von Boden und Pflanzen-/Kronendachfeuchte)
Die mathematische Beschreibung für z.B. die 6 reflektiven Bänder von Landsat TM lautet:
- Brightness = 0.3037(Band 1) + 0.2793(Band 2) + .4743(Band 3) + 0.5585(Band 4) + 0.5082(Band 5) + 0.1863(Band 7)
- Greenness = -0.2848(Band 1) - 0.2435(Band 2) - 0.5436(Band 3)+ 0.7243(Band 4) + 0.0840(Band 5) - 0.1800(Band 7)
- Wetness = 0.1509(Band 1) + 0.1973(Band 2) + 0.3279(Band 3) + 0.3406(Band 4) - 0.7112(Band 5) - 0.4572(Band 7)
Spektrale Verschneidungen (pan-sharpening, resolution merge) oben
An dieser Stelle sei angemerkt, daß die Hauptkomponententransformation auch für die Verschneidung von Fernerkundungsdaten unterschiedlicher geometrischer und spektraler Auflösung von Bedeutung ist (engl.: resolution merge, pan-sharpening). Man geht hier von dem Prinzip des Austausches der ersten HK (Gesamtalbedo) eines geometrisch gering auflösenden, aber multispektralen Datensatzes (z.B. TM) gegen einen geometrisch hochauflösenden panchromatischen Datensatz der gleichen Region (z.B. TM-pan, SPOT-X, IKONOS, Quickbird oder digitale Luftbilder) mit anschließender invers gerechneter HKA aus.
Das Prinzip soll anhand der Verschneidung eines multispektralen LANDSAT TM 5 -Datensatzes und eines panchromatischen Luftbildes aus der Pilbara-Region in Westaustralien erläutert werden (Zumsprekel & Prinz, 1998). Der ein multispektrale TM-Datensatz besitzt eine relativ geringe geometrische Auflösung von 30m/Pixel - das analoge panchromatische Luftbild jedoch eine hohe geometrische Auflösung von ca. 3m/Pixel (Abb. 3.5.8 und 3.5.9).
Nachdem das ursprünglich analoge Luftbild mittels eines Scanners digitalisiert und anschließend innerhalb des geographischen Bezugssystems der digitalen Satellitendaten rektifiziert wurde, sollen nun die Vorteile beider Datensätze in einem neu errechneten Datensatz miteinander kombiniert werden. Dabei dient das Luftbild als einkanaliger Datensatz mit hoher geometrischer Auflösung, aber fehlender multispektralen Information. Die panchromatichen Grauwerte des Luftbildes entsprechen also annähernd der Gesamtalbedo im RGB-Bereich!
 |
Abb. 3.5.8: TM IR-Falschfarben- komposite TM 5; 4; 7 [rgb] der Pilbara-Region, W.A. mit einer Pixelauflösung von 30 m (Zumsprekel & Prinz, 1998) |
 |
Abb. 3.5.9: Panchro- matisches Luftbild aus Pilbara-Region, W.A. mit einer Pixelauflösung von ca. 3 m (Zumsprekel & Prinz, 1998) |
In einem nächsten Schritt werden die rektifizierten TM 5-Daten einer HKA unterzogen, aus der sechs unterschiedliche HK's hervorgehen. Wie bereits zuvor erläutert, entspricht die 1.HK weitgehend der Gesamtalbedo aller TM-Daten. Dies ist für den Verschneidungsprozess wichtig, da nun die 1.HK durch die panchromatischen Luftbild-Daten ersetzt wird, welche ja auch als Gesamtalbedo angesehen werden kann.
Diese panchromatischen Luftbild-Daten besitzen jedoch eine 10x höhere geometrische Auflösung als die TM-HK's, so daß nach einer inversen HKA der TM-Daten ein synthetischer, multispektraler Datensatz mit einer geometrischen Auflösung von 3/Pixel und einer spektralen Bandbreite des TM's, also vom VIS bis zum IR, für das Areal des Luftbildes erzeugt wird (pan-sharpening).
Anstelle des Satellitenbildes kann nun ein kleineres Areal grossmaßstäblicher (z.B. 1 : 10.000 anstatt 1: 50.000) auf der Basis digitaler Luftbilder multispektral analysiert werden (Abb. 3.5.10).
 |
Abb. 3.5.10: Verschneidung von spektralen IR-Falschfarben (TM) mit der hoch-auflösenden panchro-matischen Luftbildaufnahme der Pilbara-Region W.A. (Zumsprekel & Prinz, 1998) |
Neben der Möglichkeit einer HKA-gestützten Verschneidung von Fernerkundungsdaten unterschiedlicher geometrischer bzw. spektraler Auflösung, wird häufig auch die RGB-IHS-RGB Transformation für einen 'resolution merge/pan-sharpening' herangezogen.
Das Prinzip ist ähnlich: Es wird keine Albedo-spezifische HK gegen die Gesamtalbedo eines hochauflösenden Datensatzes ausgetauscht, sondern die Intensitäts-Komponente (I) einer vorab definierten 3 Kanal-Kombination als Maß für die Gesamtalbedo durch den panchromatischen Datensatz (z.B. Luftbild) ersetzt. Eine anschließende IHS-RGB-Rücktransformation führt dann zu einem multispektralen Datensatz mit höherer geometrischer Auflösung.
Beachte: Bei einer RGB-IHS-RGB-Transformation stehen immer nur die zuvor ausgewählten drei Kanäle mit einer höheren geometrischen Auflösung zur Verfügung, während eine HKA-basierte Verschneidung immer alle Kanäle mit der neuen geometrischen Auflösung zugänglich macht).
Beide Verfahren sind Standardanwendungen, um die Vorteile von hochauflösenden, panchromatischen Daten eines Sensors mit seinen multispektralen Reflexionswerten zu rekombinieren. Moderne Fernerkundungssysteme (z.B. Landsat-ETM 7/8, Spot-5 , Quickbird ect.) erfassen deshalb synchron panchromatische und multispektrale Daten. Die daraus abgeleiteten Produkten werden oft kurz als ' pan-sharpened' bezeichnet
Um störende Nebeneinflüsse auf die Darstellung von Rasterdaten zu minimieren oder bestimmte geometrische Bildinhalte hervorzuheben werden darüber hinaus noch Filtermethoden eingesetzt. Diese komplexen Spektraloperationen sollen aber in einem eigenständigen Kapitel behandelt werden, da sie mathematisch andersartig wirken.