5.3 Standortbestimmung
Im vorausgegangenen Kapitel wurden die grundlegenden Meßverfahren zur Ermittlung der Entfernungen zwischen
Beobachter und Satelliten über die sog. Pseudoentfernungsmessung beschrieben.
Hier sollen nun die Verfahren der Bestimmung des Standortes und der nötigen
technischen Datenverarbeitung auf Empfängerseite knapp umrissen werden.
Technische Datenverarbeitung
Für die Pseudoentfernungsmessung ist es erforderlich, daß auf der Benutzerseite ein Empfänger die Funkverbindung zu den einzelnen Satelliten selektiv herstellt und aufrecht hält. Die in der Kommunikationstechnik übliche Selektion nach unterschiedlichen Sendefrequenzen, wie z.B. beim Radio (Frequency Division Multiplex Access = FDMA) kann nicht in Betracht gezogen werden, da alle GPS-Satelliten die gleichen Frequenzen benutzen. Deshalb wird bei GPS das Code Multiplex Verfahren (CDMA) angewandt, wobei jedem GPS-Satelliten eine bestimmte PRN-Impulsfolge zugeordnet wird, welche eine Identifikation der Satelliten trotz gleicher Sendefrequenz auf Empfängerseite ermöglicht. Einheitlich sind innerhalb der Codes lediglich Bit-Länge und -Anzahl, Taktfrequenz bzw. Länge des Codes (Mansfeld, 1998) . Zur Kontaktaufnahme mit einem speziellen Satelliten muß der Empfänger also einen passenden Identifikationscode auswählen!
Der grundsätzliche Meßvorgang beruht auf dem Prinzip der Korrelation von empfangenem und
intern erzeugtem Referenzsignal (vgl. Kap. 5.2) . Auf der
Empfängerseite wird der Meßvorgang mit der empfangenen PRN-Impulsfolge des C/A-Codes
eingeleitet. Die zeitgleich erzeugte möglichen PRN-Referenzimpulse werden mit den empfangenen Signalen
verglichen und synchronisiert, wobei bereits eine Zeitverzögerung hinsichtlich des eintreffenden
Satellitensignals ermittelt werden kann.
Erst in dem Moment, wenn erzeugte und empfangene PRN-Impulsfolgen zur Deckung kommen ist die Funkverbindung zu einem identifizierten Satelliten hergestellt! Das Kriterium zur Übereinstimmung ist die Phase der Impulsfolge (vgl. Kap. 5.2), deshalb wird dieses Verfahren auch oft Code-Phase-Verfahren genannt.
Im nötigen Korrelationsprozeß gibt es technisch gesehen drei wesentliche Arbeitschritte:
- Suchen (search): Die Phase der gewählten PRN-Impulsfolge wird kontinuierlich verschoben, bis die Übereinstimmung erreicht ist!
- Empfangen (acquisition): Jetzt ist die Funkverbindung selektiv hergestellt, die Information wird übertragen!
- Verfolgen/Nachlaufen (tracking): Da die geometrische Position von Empfänger und Satelliten ständigen Änderungen unterworfen
ist, muß die Phasenverschiebung zur Aufrecherhaltung der Funkverbindung fortlaufend nachgeregelt werden!
Obiger Prozeß vollzieht sich in Code-Phasen-abhängigen Empfängern (üblicher Empfängertyp) technisch über eine Verzögerungsregelschleife (Delay Lock Loop, DLL). Der Prozeß des Suchens, Einrastens und Nachlaufens wird auch als Nachlaufregelschleife mit zwei Grundfunktionen bezeichnet (Abb. 5.3.1) :
- Verzögerungsregelschleife (DLL) , auch Code-Regelschleife genannt (Code Tracking Loop)
- Phasenregelschleife (Phase Lock Loop = PLL)
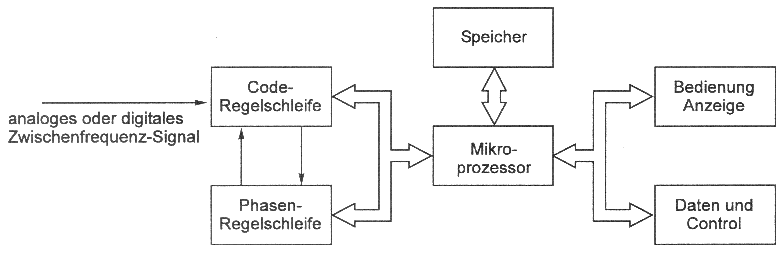
Abb. 5.3.1: Schematisches Funktionsschaltbild eines codeabhängigen GPS-Empfängers mit DLL- bzw. PLL-Schleife (Mansfeld, 1998)
Der Korrelationsprozeß des P-Codes würde aufgrund der sehr großen Länge (267 Tage) normalerweise zu lange dauern und die Funktionalität des Empfängers stark einschränken. Deshalb wird bei authorisierten codeabhängigen P-Code-Empfängern in die intern erzeugte PRN-Impulsfolge eingegriffen, so daß grundsätzlich Impulsfolgen erzeugt werden, die bereits nahe am Ursprungscode der jeweiligen Satelliten liegen. Dies wird durch ein "Übergabewort" (Hand Over Word = HOW) gewährleistet, welches aus der Navigationsnachricht des bereits bearbeiteten C/A-Codes stammt.
Sobald der Korrelationsvorgang des C/A- (P-) Codes beendet ist, kann die Trägerfrequenz durch Mischung/Überlagerung mit der eigenen internen Frequenz und nachfolgender Filterung eleminiert werden, so daß nur die aufmodulierte Navigationsnachricht erhalten bleibt und die unmodulierte Trägerphase in ihrer Zeitverzögerung durch Phasenwinkelverschiebung gemessen werden kann. Erst jetzt beginnt die eigentliche Positionsbestimmung!
Es sei an dieser Stelle darauf hingewiesen, daß es code-unabhängige GPS-Empfänger gibt, welche für sehr spezielle Anwendungen konzipiert sind. Die Positionierung über Laufzeitunterschiede erfolgt hier meist über das sog. Quadrierungsverfahren bzw. die interferometrische Auswertung von Signalfolgen. Code-unabhängige GPS-Empfänger spielen in der zivilen Breitennutzung bisher keine große Rolle!
Geometrische Standorte
Die Berechnung des Standortes auf der Basis der GPS-Navigationsdaten und Pseudoentfernungen erfolgt durch Einpassung und Umrechnung der GPS-spezifischen Beobachtungsgrößen in ein raumfestes Bezugssystem (vgl. Kap. 1.2) . Für die Beschreibung der Bewegung von Himmelkörpern hat der Astronom Johannes Kepler im 17. Jahrhundert wichtige Grundlagen geschaffen und verifiziert. Da Satelliten künstliche Trabanten der Erde darstellen, gelten diese Gesetzmäßigkeiten auch für sie in einem raumfesten, inertialen Bezugssystem (CIS)!
Merke: Ein Inertialsystem ist ein Bezugssystem, dessen Achsen raumfest sind und dessen Ursprung keiner Beschleunigung ausgesetzt ist!
Zur Beschreibung von Satellitenbewegungen benutzt man ein entsprechedes geozentrisches Inertialsystem mit seinem Ursprung im Massenzentrum der Erde, dem sog. Geozentrum (Brinkkötter-Runde, 1995) . Auf der Erdoberfläche befindliche Standorte sind jedoch ständig in Bewegung (Erdrotation), so daß für die lokale Ortsdefinitionen ein vereinbartes erdfestes Bezugssystem (CTS) definiert werden muß (Abb. 5.3.2).
Es ist wie folgt definiert (vgl. Kap. 1.2):
- Koordinatenursprung liegt im Geozentrum
- Z-Achse beschreibt die Rotationsachse der Erde
- X-Z-Ebene wird durch die Z-Achse und der Position der Sternwarte von Greenwich definiert (historisch bedingt)
- Y-Achse folgt aus der 90°-Drehung der X-Achse
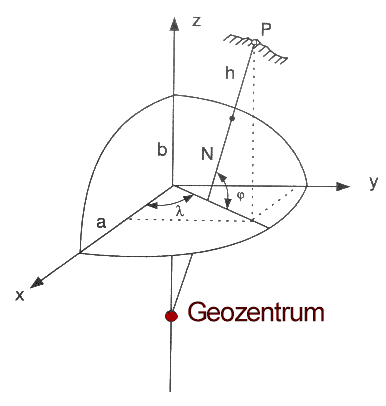
Abb. 5.3.2: Das inertiale CTS-System mit kartesischen Koordinaten bzw. ellipsoiden Winkel-Koordinaten (modifiziert nach (Mansfeld, 1998)
Für eine Transformation von Koordinaten des Inertialsystems in das terrestrische Koordinaten we rden ein System astronomischer Konstanten, Rotationsmatrizen für Nutation und Präzession (Schwankungen der Erdachsenlage) sowie Zahlenwerte zur Beschreibung der geophysikalischen Eigenschaften der Erde (Dichte, Massenverteilung...) benötigt. Zusammen mit weiteren Ellipsiodparametern definieren sie ein geodätisches Referenzsystem, welches für das GPS definitionsgemäß das 1984 berechnete WGS-84 darstellt. Seit 1987 werden auch die Ephemeriden der Satelliten in Bezug zum WGS-84 gesetzt, so daß sich sämtliche Koordinaten und deren relativen Unterschiede, die mit dem GPS bestimmt werden, diesem Bezugssystem zugrunde liegen (Hofmann-Wellenhof et al., 1994).
Die Parameter des WGS-84 sind so gewählt, daß es sich als Referenzellipsoid der Erdfigur bestmöglich anpaßt. Dabei wird angenommen, daß der Erdmittelpunkt mit dem tatsächlichen Erdschwerpunkt (Massenmittelpunkt) zusammenfällt. Zur weiteren Definition gehören die Erdschwere, die Winkelgeschwindigkeit der Erde und die Gravitationskonstante:
| Parameter | Bezeichnung | WGS-84 |
| Große Halbachse | a | 6378137 m |
| Abplattung | f | 1 / 298,257223563 |
| Winkelgeschwindigkeit | ω | 7,292115 x 10 -5 rad s -1 |
| Gravitationskonstante | GM | 398600,5 km 3 s -2 |
| 2. zonale harmonische Kugelfrequenz | J 2 | 484,16685 x 10 -6 |
In Anlehnung an Kapitel 1.3 werden in Kenntnis des oben beschriebenen GPS-Referenzsystems für eine dreidimensionale Positionsbestimmung auf der Erdoberfläche (mathematisch) drei Satelliten benötigt, deren jeweiligen Pseudoentfernungen zum Empfänger gemessen werden. Bei einer Messung mit nur einem Satelliten würde sich der Beobachter irgendwo auf einer Signalkugelfläche (-sphäre) um den Satelliten befinden. Bei zwei verwendeten Satelliten ist die Nutzerposition im Schnittkreis (-fläche) der zwei Sphären zu finden. Die Hinzunahme eines dritten Satelliten führt dann endgültig zu einem theoretischen Schnittpunkt mit eindeutigen Lagekoordinaten (die in der Praxis auftretende Fehler bleiben hier unberücksichtigt; vgl. auch Kap. 2.4!).
Der Empfängerstandort ist also der Schnittpunkt der Satellitensphären, deren jeweilige Radien durch die Pseudoentfernungen definiert sind. Es läßt sich daher ein einfaches Gleichungssystem auf der Basis der allgemeinen Kreisgleichung aufstellen, um die gewünschten Koordinaten zu berechnen (s.u.). Da jedoch neben dem bisher unbekannten Ort auch der Uhrenfehler berechnet werden muß, wird eine vierte Gleichung (und auch vierter Satellit!) zur vollständigen Lösung beider Probleme benötigt:

modifiziert nach Brinkkötter-Runde (1995)
Es wird deutlich, daß mit Ausnahme der Koordinaten des Benutzerstandortes im WGS-84 System (also X,Y und Z) alle Variablen (nach Korrektur evtl. Fehler) durch das GPS über die bisher beschriebenen Analyseverfahren ermittelt werden können. Obige Gleichung wird nun nach X-, Y- und Z-Koordinaten aufgelöst, womit der Beobachtungsort bzgl. WGS-84 bestimmt ist!
Die ermittelten Koordinaten liegen nun im universellen WGS-84 Bezugsystem vor und müssen daher für viele Anwendungen in ein lokales Bezugssystem (nach jeweiligem Kartendatum) transformiert werden. Wie dies geschieht, erläutert das folgende Kapitel...
