5.2 Signallaufzeit und Trägerphasenmessung
Bei Berechnung der Pseudoentfernungssphären um die GPS-Satelliten werden vier verschiedene
Beobachtungsgrößen unterschieden:
- Pseudoentfernungen aus Codemessung (vgl. Kap. 5.1)
- Pseudoentfernungsdifferenzen aus intergriertem Doppler-Count
- Pseudoentfernungen aus Trägerphase oder Trägerphasendifferenz
- Signallaufzeitdifferenzen aus interferometrischer Messung
Die Pseudoentfernung aus Codemessungen wird vor allem zur schnellen Positionierung genutzt (Mansfeld, 1998) . Die Messung der Trägerphase wird wegen der erzielbaren größeren Genauigkeit zur Lösung statischer, meßtechnischer Aufgaben (Geodäsie) verwendet. Heute kommen jedoch vielfach kombinierte Auswerteverfahren zum Einsatz, wobei auch Signallaufzeiten und Doppler-Effekte zur Bestimmung des momentanen Ortes und der Pseudoentfernungen bzw. Geschwindigkeiten herangezogen werden. Außerdem liefert die Auswertung der Meßergebnisse der Pseudoentfernung und der Navigationsmitteilungen die nötige Zeitinformation.
Signallaufzeiten
Die Signallaufzeit zwischen Satellit i und dem Beobachtungspunkt j ergibt sich unter Einbeziehung der möglichen (Fehler-) Parameter (vgl. Kap. 4.2) über die komplexe Beziehung (Brinkkötter-Runde, 1995) :

Für die Bestimmung einer dreidimensionalen Position sind vier Entfernungsmessungen durch den obigen Formelansatz notwendig, da über die vierte Messung die Zeitdifferenz zwischen Satelliten- und Empfängeruhr ermittelt wird (Uhrenfehler!).
Trägerphasenmessung
Neben der codeabhängigen und signallaufzeitabhängigen Berechnung von Pseudoentfernungen spielt besonders die trägerphasengestütze Berechnung von Entfernungen eine große Rolle in der geodätischen GPS-Technik. Der wesentliche Unterschied zwischen den Beobachtungsansätzen ist die Einbeziehung eines Mehrdeutigkeitsfaktors (n), da die exakte Entfernungsmeßung über Trägerphasenwinkel nur innerhalb einer Länge eindeutig wäre, welche genau über die Wellenlänge der Trägerfrequenz definiert ist.
Die Beziehung zwischen Phase, Laufweg und Wellenlänge ist durch folgende Gleichung gegeben (vgl. Kap. 4.1) : δs = δΦ / 2 φλ
Die Phase wiederholt sich im Abstand von 2 φ bzw. im Abstand genau einer Wellenlänge. Es kann daher geschrieben
werden:
( δΦ + n 2 φ) / 2 φ = ( δs + n λ) / λ
(wobei n = 0, 1, 2, 3....)
Für die Bestimmung einer Entfernung durch Messen der Phasen(-winkel)differenz gilt deshalb: s = (δs + n λ) = ( δΦ + n 2 φ) λ / 2 φ
Die Phasendifferenz ist somit also nur innerhalb einer Entfernung gleich einer Wellenlänge eindeutig! Der Parameter n bezeichnet den Mehrdeutigkeitsfaktor !
Zur Bestimmung der Entfernung wird die Differenz Φm des Phasenwinkels ΦTr der empfangenen Trägerschwingung im Verhältnis zum Phasenwinkel Φ0 der empfängereigenen Referenzschwingung gemessen (Abb. 5.2.1) : Φm = Φ Tr - Φ 0
Die Referenzschwingung hat die gleiche Frequenz wie die Trägerschwingung, unterscheidet sich jedoch durch en Uhrenfehler über eine sog. Nullphasenverschiebung voneinander.
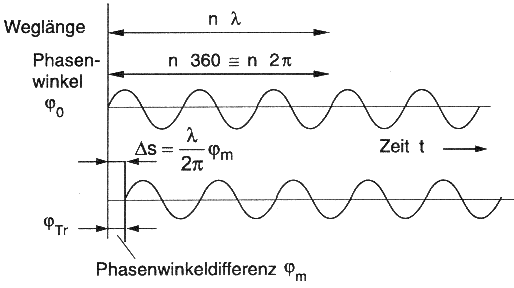
Abb. 5.2.1: Phasenwinkeldifferenz von Träger- und Referenzschwingung (Mansfeld, 1998)
Die mit der Phasendifferenzmessung mit Hilfe der Referenzschwingung verbundenen Meßfehler lassen sich reduzieren, wenn die Phasendifferenz der Trägerschwingung des gleichen Satelliten von zwei oder mehreren unabhängigen Empfängern gemessen wird. Dabei müssen sich die Empfänger A und B... einen räumlichen Abstand groß zur Wellenlänge befinden. Als Nebeneffekt lassen sich so auch die Dopplereffekte der Trägerphase besser korregieren. In der Geodäsie werden deshalb immer Netze von GPS-Stationen aufgebaut, welche ihre Phasendifferenzmessungen während Dauermessungen aufeinander abstimmen.
Die tatsächlich beobachtete Trägerphase zum Zeitpunkt (t) wird unter Berücksichtigung aller Einflußgrößen wie folgt berechnet (Brinkkötter-Runde, 1995) :
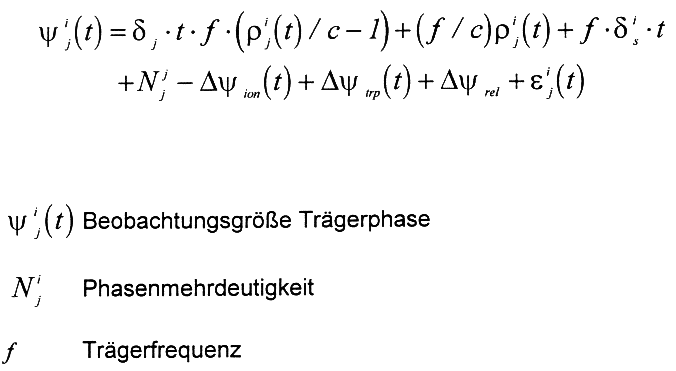
Doppler-Count
Neben den oben beschriebenen Berechnungsmöglichkeiten von Pseudoentfernungen kann eine Entfernungsmessung auch über die Doppler-Frequenzverschiebung(-count) vollzogen werden. Bei einigen GPS-Empfängern spielt auch diese Technik eine gewisse Rolle und soll deshalb hier nur in ihren Grundzügen kurz erläutert werden.
Die Doppler-Frequenzverschiebung tritt auf, wenn in einer Funkverbindung zwischen Sender und Empfänger eine Relativgeschwindigkeit besteht. Da sich die Entfernungen zwischen GPS-Empfänger und Satelliten innerhalb eines Zeitraumes ständig ändern, ist dies auch hier der Fall. Es können die Frequenzverschiebungen des empfangenen Trägers mit der Frequenz f e mit Bezug auf die konstante Frequenz f g einer im Empfänger erzeugten hochfrequenten Schwingung im Zeitintervall t 1 bis t 2 beobachtet und ausgewertet werden.
Ihre Integration über die Zeit führt zu dem integrierten Doppler-Count : C d = ∫(f g - f e) dt
C d ist ein Maß für die Entfernungsdifferenz zwischen dem Empfänger und zwei Bahnpositionen desselben Satelliten S i zu zwei verschiedenen Zeitpunkten t 1 bzw. t 2 (Abb. 5.2.2). Für die Entfernungsdifferenz ergibt sich so: δρi = c /f s [C d - (f g - f e)(t 2 - t 1)]
; wobei c = Ausbreitungsgeschwindigkeit der Welle, f s = Frequenz des Trägers, f g = Frequenz des Empfängers, f e = Frequenz des empfangenen Trägers und t 1 bzw. t 2 die Zeitpunkte repräsentieren.
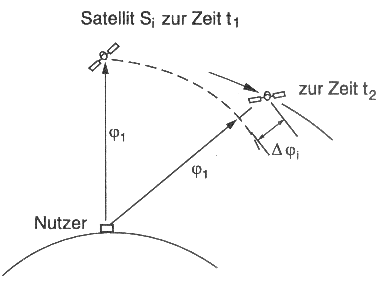
Abb. 5.2.2: Geometrische Beziehungen bei der Bestimmung der Entfernungsdifferenz über Trägerfrequenzverschiebungen (Mansfeld, 1998)
Prinzipiell ist es auch möglich, die Doppler-Frequenzverschiebung über die PRN-Impulsfolge des GPS-Codes zu messen. Allerdings ist die Taktfrequenz von etwa 1 bzw. 10 MHz um das 100- bzw. 1000-fache kleiner gegenüber dem hochfrequenten Träger L 1 = 1575,42 MHz; die Auflösung der Messung wäre also zu gering.
