5.4 Transformationen
Im vorangegangenen Kapitel sind die grundlegenden Zusammenhänge zwischen astronomischen und terrestrischen
Koordinatensystemen erläutert worden. Die Abbildung der Koordinaten des WGS-84 in Bezugssystemen
der Landesvermessung (z.B. UTM, Gauß-Krüger) wird über ellipsoidische Koordinaten,
jeweils bezogen auf das geltende Referenzellipsoid, vollzogen
(Brinkkötter-Runde, 1995) .
Um dreidimensionale kartesische GPS-Koordinaten in dieses System einbinden zu können, müssen jene also in ellipsoidische Koordinaten umgerechnet werden, wobei das System im Bedarfsfall auch den umgekehrten Weg gehen können sollte.
Kartesische und ellipsoidische Koordinaten
Nach Seeber (1989) wird die Form der Erde mathematisch am besten durch ein an den Polen abgeplattetes Rotationsellipsoid mit Höhenabweichungen von < 100m zum Geoid an den Polen beschrieben. Das Rotationsellipsoid basiert auf der Drehung der Meridianellipse (große Halbachse) um ihre kleine Halbachse.
Ihre Geometrieeigenschaften sind deshalb wie folgt definiert:
Abplattung = f = (a - b) / a
1. num. Exzentrität = e 2 = (a 2 - b 2 ) / a 2
mit a = große und b = kleine Halbachse des Ellipsoids)
In den alten Bundesländern (West-Deutschland) wird in der Landesvermessung das Ellipsoid nach Bessel (a = 6377397,155m; f = 299,1528) für das Deutsche Hauptdreiecksnetz (DHDN) verwendet. Fundamentalpunkt ist der heute nicht mehr existierende Trigonometrische Punkt (TP) Rauenberg in Berlin, an dessen Stelle formal der TP Potsdam getreten ist. Potsdam ist somit das gültige Bezugsdatum mit astronomisch/geophysikalisch neu eingemessenen Längen-, Breitenwerten bzw. gravimetrischen Konstanten. Alle Basislinien der Grundvermessung sind am Potsdamer geodätischen Datum orientiert und zukünftig für die gesamtdeutsche Landesvermessung maßgeblich.
In den neuen Bundesländern (Ost-Deutschland) gilt aufgrund der historischen Entwicklung noch das Parallelsystem nach dem Krassovski-Ellipsoid osteuropäischen Ursprunges (Datum Pulkovo/St. Petersburg) . Es basiert auf dem astronomisch geodätischen Netz der ehem. DDR (AGN). Alle neuen Vermessungen erfolgen in den neuen Bundesländern bereits nach Gauß-Krüger/Potsdam-System, so daß oft geodätische Werte in beiden Bezugsräumen vorliegen können! Die Abweichungen zwischen den beiden Netzen können bis zu 500m betragen (Seeber ,1989)!
Die Beziehung zwischen kartesischen (x, y, z) und ellipsoidischen Koordinaten
(λ, Φ, h ) ergibt sich durch:
x = (N + h) cos Φ cos λ
y = (N + h) cos Φ sin λ
h = (b 2 /a 2 + h) sin Φ
mit:
λ = geographischer Längengrad
Φ = geographischer Breitengrad
h = ellipsoidische Höhe in Metern
N = Querkrümmungshalbmesser
N = a 2 / (a 2 cos 2 Φ+ b 2 sin 2 Φ ) 0,5
Die Umkehrung dieser Formeln zur Brechnung ellipsoidischer Koordinaten aus kartesischen Koordinaten kann mit
ausreichender Annäherung (in Vermeidung iterativer mathematischer Prozesse) durch nachfolgende Formeln
(Hofmann-Wellenhof et al., 1992) vollzogen werden:
Φ = arctan [(Z + e' 2 b sin 3 φ ) / (p - e 2 a cos 3 φ)]
λ = arctan x/y
h = p / cos Φ - N
mit:
φ= arctan Za / pb = Hilfsgröße zur Vermeidung der iterativen Verfahren
e' 2 = (a 2 - b 2 ) / b 2 = 2. num. Exzentrität
p = (x 2 + y 2 ) -2 =Parallelkreisradius
Da die GPS-Koordinaten im globalen WGS-84 Bezugssystem eingebettet sind, müssen die Beziehungen zwischen diesem und dem der Landesvermessung zugrundeliegenden System bekannt sein (Brinkötter-Runde, 1995). Die Beziehung zwischen einem lokalen Ellipsoidmodell und dem globalen geodätischen Bezugssystem nennt man Geodätisches Datum; der Übergang zwischen den Systemen wird Datumstransformation genannt.
Das WGS-84 und das Potsdamer Datum unterscheiden sich in den Punkten:
- Maßstab
- Richtung des Koordinatensystems
- Koordinatenursprung
Die Transformation vom Satellitendatum in das lokale Datum erfolgt deshalb über eine
- Änderung des Maßstabes
- Rotation um x-, y- und z-Achse
- Verschiebung des Koordinatensystems um δx, δy und δz
Transformationen
Mathematisch betrachtet erfolgt die Berechnung des Datumsüberganges aus praktischen Gründen innerhalb der kartesischen Systeme beider Daten (Seeber, 1989) . Aufgabe der Landesvermessung ist es also, die nach dem Geodäten Fried.-Joh. Helmert (1843-1917) benannte erforderliche 7-Parameter-Transformation (Helmert-Transformation) umzusetzen. Dies sind neben den drei Datumsverschiebungskonstanten ( δx, δy und δz) die drei Achsenrotationsparameter (εx , εy, εz) und der Maßstabsfaktor (m).
Nach Regeln der analytischen Geometrie gilt dann (vgl. Abb. 5.4.1) :
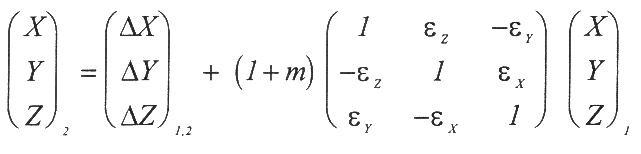
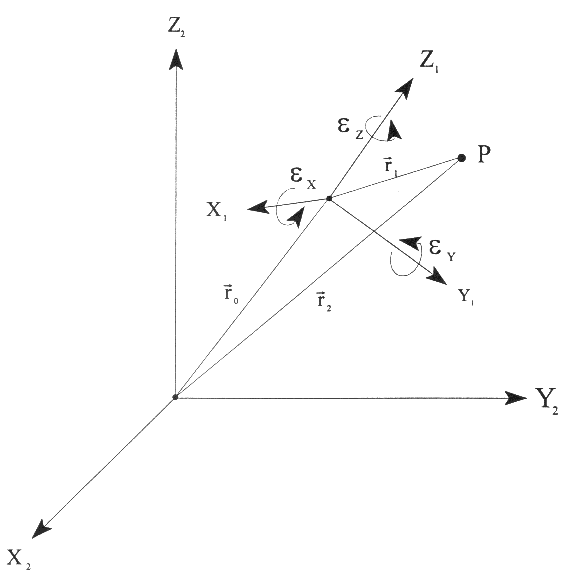
Abb. 5.4.1: Schematische Darstellung des Datumsüberganges im kartesischen System (Seeber, 1989)
Die Translationsvektoren (r) sind unterschiedliche Positionsvektoren in Bezug zum gemeinsamen Beobachtungspunkt P !
Die Bestimmung der Transformationsparameter wird über identische Punkte des Deutschen Referenznetzes (DREF) umgesetzt. Die Koordinaten der identischen Punkte sind im WGS-84 und im Potsdamer Datum (System 42 für die neuen Bundesländer) bekannt, so daß die nötigen Transformationsparameter abgeleitet werden können (Brinkötter-Runde, 1995).
In Tabelle 5.4.1 sind die Transformationsparameter nach Ihde & Lindstrot (1995) mit einer mittleren Genauigkeit von 5 m angegeben.
| Parameter | DHDN/WGS-84 | S42/WGS-84 |
| δx | + 582 m | + 24 m |
| δy | + 105 m | - 123 m |
| δz | + 414 m | - 94 m |
| εx | + 3,08'' | + 0,13'' |
| εy | - 0,35'' | + 0,25'' |
| εz | - 1,04'' | - 0,02'' |
| m | + 8,3 x 10 -6 | + 1,1 x 10 -6 |
Tab. 5.4.1: Transformationsparameter in Bezug zum WGS-84 (Ihde & Lindstrot ,1995)
Nach der Transformation müssen die Koordinaten in ein ebenes, rechtwinkliges Karten-Koordinatensystem, z.B. das Haupkartenwerk NRW mit Gauß-Krüger-System überführt werden. Das GK-System beruht auf einer transversalen Mercatorprojektion, dessen Zentralmeridian die 3-Grad-breiten Streifen in der Mitte teilt (vgl. Kap. 1.1) .
Der in der Mitte projezierte Zentralmeridian wird ohne Verzerrung wiedergegeben und repräsentiert die y-Achse des Koordinatensystems (Hochwerte!). Die x-Achse (Rechtswerte!) wird durch den Äquator abgebildet. Über eine Reihenentwicklung können aus elliptischer Länge und Breite der Rechts- und Hochwert des GK-Systems ermittelt werden:
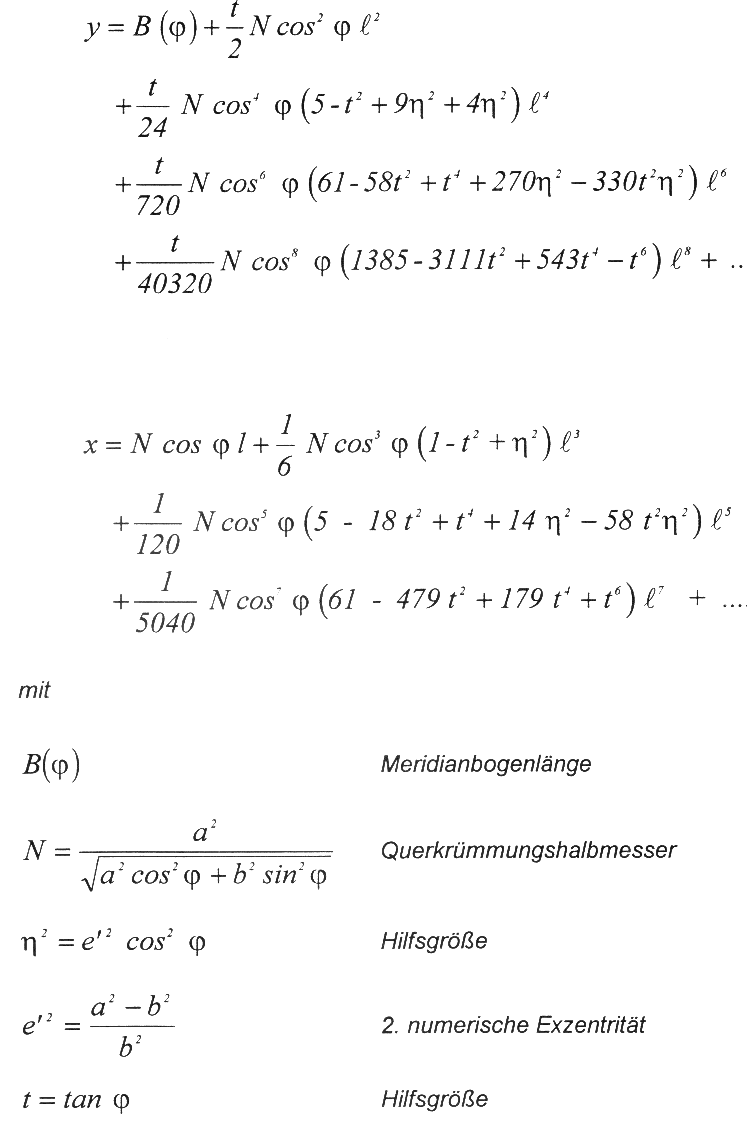
Die Meridianbogenlänge (B) wird in Abhängigkeit von der geographischen Breite über das Integral B ( λ) berechnet. Sie gibt die Ellipsoiddistanz zwischen Äquator und beobachteten Punkt wieder. Das Integral läßt sich durch eine Reihenentwicklung gut auflösen:

Zur Vermeidung von negativen Koordinaten der westlich des Zentralmeridians liegenden Punkte wird dem Rechtswert im GK immer 500.000 (m) hinzugrechnet (vgl. Kap. 1.1). Nach Durchführung der Transformation und anschließender Datumsüberführung in die Gaus-Krüger-Abbildung, liegen die GPS-Koordinaten in der benötigten lokalen Bezugsebene des topographischen Kartenwerkes vor und können so in die Weiterverarbeitung von Geodaten miteinbezogen werden.
GPS-Empfänger verfügen meist über einen mehr oder minder umfangreichen Katalog von möglichen Bezugsdaten, wobei die im WGS-84 errechneten Positionen dann automatisch in das jeweilige lokale System umgerechnet werden. Leider sind die im Gerät implementierten Algorithmen zur Transformation meist nicht dokumentiert, so daß sich auch hier Ungenauigkeiten ergeben können, welche vom Nutzer unabhängig sind und nicht korrigiert werden können (z.B. vereinfachte Transformationsalgorithmen für einen ganzen Kontinent oder einzelne Staaten).
