4.1 Wellenstruktur
Das Medium zur Bereitstellung der Ortungsinformation für das GPS ist die elektromagnetische Welle!
Sie ist aus einem elektrischen und magnetischen Feldvektor zusammengesetzt, welche immer aufeinander senkrecht
stehen. Die Welle hat grundsätzlich das Bestreben, sich in einer
bestimmten Richtung auszubreiten, wobei diese Richtung senkrecht zu den beiden Vektoren orientiert ist
(Abb. 4.1.1).
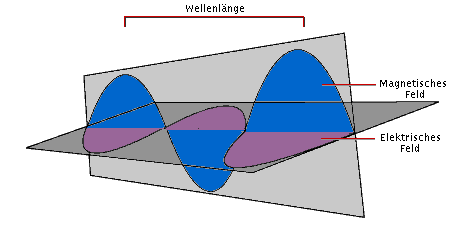
Abb. 4.1.1: Die elektromagnetische Welle als Kombination von magnetischen und elektrischen Feldvektoren
Strukturen
Eine sich ausbreitende periodische Welle (vgl. Abb. 4.1.1) ist durch die Wellenlänge ( λ), die Frequenz (f ) und die Geschwindigkeit (v ) definiert. Es gilt: v = λf
Die Periodizität der Welle ist durch einen definierten Zustand gekennzeichnet, welcher sich an einem gegebenen Ort und nach einer bestimmten Zeit in einer bestimmten Entfernung wiederholt. Diese Entfernung ist die Wellenlänge ( λ). Die Periodizität wird als Periode (T ) angegeben; sie ist reziprok zur Frequenz f (Mansfeld, 1998): T = 1 / f
Der Bruchteil der Periodendauer (T) ist die Phase (Φ) der periodischen Welle. Der zeitliche Verlauf der Welle läßt sich auch durch die Winkelgeschwindigkeit (Ω) angeben (Kreisfrequenz): Ω = 2 π f
Die Ausbreitungskonstante (γ) der Welle ist: γ = α+ j β
wobei α die Dämpfungskonstante und β die Phasenkonstante ist; für Letztere gilt: β = 2 π / λ
Für die Ausbreitungsgeschwindigkeit (v) kann deshalb auch die Beziehungsfolge geschrieben werden: v = λ / T = f λ = ( λ 2 π f ) / 2 π = 2 π f / β= Ω / β
In der Funktechnik werden elektromagnetische Wellen durch Sinusfunktionen dargestellt. Der Momentanwert (a) eines bestimmten periodischen Zustandes zur Zeit (t) ist gleich: a = A sin 2 π (t / T + Φ 0 )
A ist gleich der Amplitude und Φ 0 die Phase zur Zeit t = 0. Die Phase zur Zeit (t) ist dann gleich: Φ = t / T + Φ 0
Das Argument der Sinusfunktion ist der Phasenwinkel (Φ); für ihn gilt: Φ0 = 2 Φ Φ 0 bzw. Φ= 2 πΦ
Daraus folgt: a = A sin (Ω t + Φ 0)
Die Phase der elektromagnetischen Welle dient zur Definition der Ausbreitungsrichtung und ist somit zeit- bzw. raumabhängig; der Zustand einer konstanten Phase setzt sich mit v in eine Richtung fort! Die Ausbreitungsrichtung liegt senkrecht zur Wellenfront!
Die Wellenfront wird als Ebene verstanden, auf der die Welle die gleiche Phase besitzt; man bezeichnet die Wellenfront deshalb auch als Phasenfront. Die Ausbreitungsgeschwindigkeit der Welle und die Wellenlänge sind abhängig von den elektrischen Eigenschaften des Ausbreitungsmediums (Mansfeld, 1998).
Zur Betrachtung des Phasenwinkels ist es zweckmäßig, die Gleichung zu erweitern: a = A sin ( Ω t - Ω s / v + Φ 0 )
Dabei ist s die vom Sender zum Empfänger durchlaufene Strecke und v die Ausbreitungsgeschwindigkeit der Welle bzw. Φ0 der Phasenwinkel zur Zeit t 0 . Der in Klammern stehende Term repräsentiert den Phasenwinkel an einem Beobachtungsort zur Zeit t .
Der Phasenwinkel ist somit abhängig von:
- dem durchlaufenen Zeitraum
- der Entfernung zum Beobachtungsort
- dem Anfangsphasenwinkel
Befinden sich Sendeort und Empfangsort in Ruhe, ändert sich der Phasenwinkel periodisch mit der Zeit (Abb. 4.1.2). Erfolgt die zeitgleiche Messung an Orten, welche sich mit der Geschwindigkeit v in Bezug zum Sendeort verändern, gilt: a = A sin ( Φk + Φ0 - Ω s / v )
( Φk + Φ 0 ) stellen den zum Zeitpunkt der Messung bestehenden Phasenwinkel dar. Der gesamte Phasenwinkel hängt in diesem Fall lediglich von der Länge der durchlaufenen Wegstrecke s ab!
Mit diesem Bezug ist es möglich allein durch die Phasenwinkelmessung die Entfernung zwischen Beobachtungsort und Sender zu bestimmen! Für die Entfernung gilt dann: Δs = ΔΦ / 2 πλ
Da der Phasenwinkel nicht absolut gemessen werden kann, wird die Differenz gegenüber dem Phasenwinkel einer Bezugsschwingung gleicher Frequenz gemessen (Abb. 4.1.2).
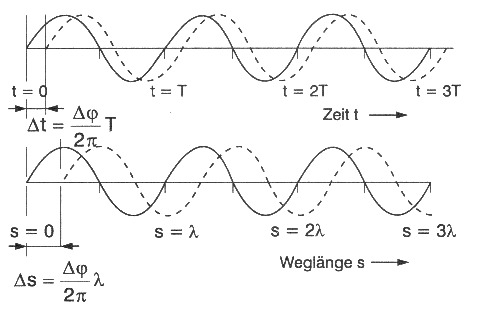
Abb. 4.1.2: Beziehung zwischen Zeit und Wegstrecke einer sich ausbreitenden elektromagnetische Welle (Mansfeld, 1998)
Die elektromagnetische Welle ist außer von Frequenz, Wellenlänge, Amplitude und Phase zusätzlich durch ihre Polarisation gekennzeichnet (Mansfeld, 1998). Besitzt der Vektor eines elektrischen Feldes an einen beliebigen Raumpunkt eine konstante Richtung, so gilt die Welle als linear polarisiert (Abb. 4.1.3a), wobei die Vektorrichtung die Polarisationsrichtung repräsentiert.
Meistens werden horizontale (H-polarisierte) und vertikale (V-polarisierte) Polarisationen zur linearen Ausrichtungen der Vektoren genutzt. Für Signalsender und -empfänger müssen die Antennen gemäß der Polarisation ausgerichtet und dimensioniert sein (Abb. 4.1.3 a,b). Bei Satelliten im Orbit ist dies nur sehr schwer realisierbar, deshalb wählt man hier die zirkulare Polarisation. Hier beschreibt die Spitze des elektrischen Vektors an einem festen Ort einen Kreis (Abb. 4.1.3 c), wobei der zirkular polarisierte Feldvektor als Resultierende aus zwei senkrecht zueinander stehenden, linear polarisierten Vektoren mit einer Phasenverschiebung von 90° gesehen werden kann (Abb. 4.1.4).
Eine einfache Antenne für das zirkular polarisierte Signal wäre eine rechtwinklig gekreuzte HV-Antenne mit geregelter 90°-Phasenverschiebung (Abb. 4.1.3 d). Eine Ausrichtung der Antenne ist in Bezug zur Polarisation nicht nötig. Technisch ausgefeilte Systeme nutzen jedoch oft Wendel- oder Spiralantennen (Abb. 4.1.3 e). Auch das GPS-System verwendet derartige richtungsunabhängig polarisierte, elektromagnetische Wellen zur Signalübertragung!
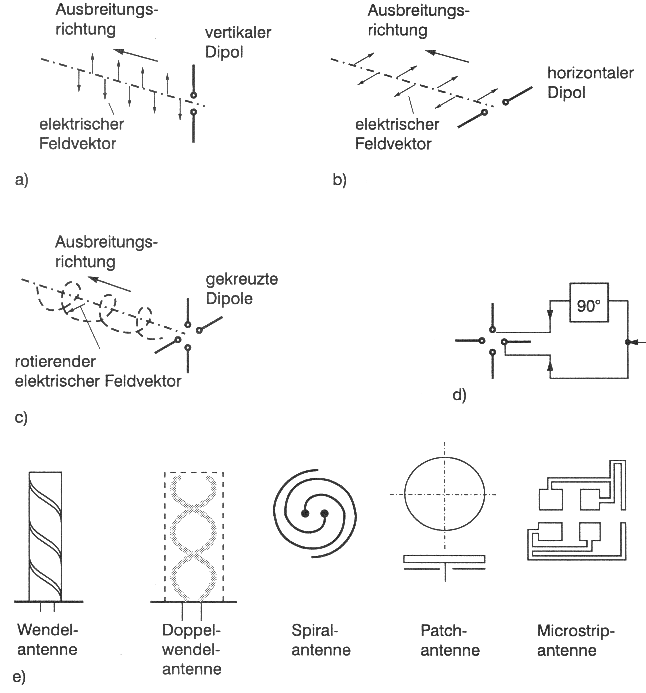
Abb. 4.1.3a-e: Verschiedene Antennentypen zum Empfang (z.T. richtungslos) polarisierter
elektromagnetischer Wellen (Mansfeld, 1998)
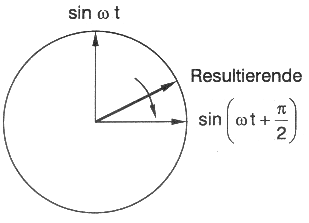
Abb. 4.1.4: Entstehung einer zirkular polarisierten elektromagnetischen Welle (Mansfeld, 1998)
Glossar: Griechisches Alphabet

