4.2 Wellenausbreitung
Elektromagnetsiche Wellen sind Träger der Information in der Funk- und Satellitenortung. Es ist
deshalb wichtig, sich über die Ausbreitungsmechanismen und deren Parameter während einer Messung
im Klaren zu sein. Die wichtigsten Parameter werden hier kurz erläutert.
Ausbreitungsgeschwindigkeit
Im freien Raum (also im Vakuum) breitet sich elektromagnetische Strahlung mit Lichtgeschwindigkeit (c) aus. Es gilt: c = λ0 / T wobei λ0 Wellenlänge im Vakuum ist.
Der Zahlenwert der Lichtgeschwindigkeit wurde 1984 durch unterschiedliche direkte oder indirekte Meßmethoden für Probleme der GPS-Satellitennavigation/-ortung auf den Zahlenwert c = 2,99792458 x 10 8 m/s festgelegt (Mansfeld, 1998). Die Genauigkeitsangabe mit acht Dezimalstellen ist nötig, da im GPS Entfernungsdifferenzen/-laufzeitunterschiede in vergleichbarer Dimension gemessen werden!
Da die elektromagnetischen Wellen auch die Atmosphäre durchlaufen, muß ihre Ausbreitungsgeschwindigkeit (v) im Nichtvakuum betrachtet werden. Hier spielt die Brechzahl (n), (sog. Refraktionszahl) eine wesentliche Rolle: n = c / v = λ0 / λ
Der Zahlenwert der Brechzahl liegt fast immer nahe 1; es ist deshalb aus praktischen Gründen wichtig mit einer normierten Brechzahl (n') zu rechnen: n' = (n-1) x 10 6
Ein Medium, in welchem sich die Ausbreitungsgeschwindigkeit von der Frequenz der Welle ableiten läßt, heißt dispersives Medium (also Dispersion von v ). Für Frequenzen größer 1000 MHz stellt insbesondere die Ionosphäre ein dispersives Medium (vgl. Kap. 2.4) dar. Die Troposphäre ist davon weitgehend ausgenommen, obwohl im Lichtwellenbereich umgekehrte Verhältnisse herrschen!
Da auch die Brechzahl von der Frequenz der Welle abhängig ist, hängt die konkrete Form der Dispersion von der Welle und dem Medium ab (komplexe Wechselwirkungen!). Die Größenordnung der Dispersion läßt sich deshalb durch den Differentialquotienten von Geschwindigkeit und Wellenlänge angeben:
D v = d v / d λZwei benutzte Wellenarten sind bei den GPS-Satellitenortungssystemen zu betrachten:
- die Einzelwelle mit einer Frequenz
- eine Wellengruppe, welche aus der Überlagerung von zwei oder mehreren Wellen mit unterschiedlichen Frequenzen besteht
Für die Ausbreitungsgeschwindigkeit einer einzelnen Welle ist das Kriterium ein bestimmter momentaner Zustand der Welle, welcher durch die Phase angegeben wird. Man bezeichnet deshalb die Ausbreitungsgeschwindigkeit auch als Phasengeschwindigkeit (v p ): v p = c / n
Für die Ausbreitungsgeschwindigkeit einer Wellengruppe ist das Kriterium der Überlagerungszustand der Gruppe, daher wird die Ausbreitungsgeschwindigkeit als Gruppengeschwindigkeit ( v g ) bezeichnet. Zwischen Phasen- und Gruppengeschwindigkeit besteht folgende Beziehung: v g = v p - λ d v / d λ
Die Gruppengeschwindiglkeit ist stets kleiner als die Phasengeschwindigkeit, wobei die Phasengeschwindigkeit in einem dispersiven Medium größer als die Lichtgeschwindigkeit sein kann! In einem nichtdispersiven Medium gilt v p = vg!
Die Gruppengeschwindigkeit gibt an, mit welcher Geschwindigkeit eine hochfrequentes Welle übertragen wird. Eine mit niederfrequenten Signalen modulierte hochfrequente Trägerschwingung stellt eine solche Welle dar. Sie setzt sich aus der Summe von Einzelschwingungen mit unterschiedlicher Frequenz zusammen. Durchläuft ein derartiges hochfrequentes Signal ein dispersives Medium, erfahren die einzelnen Schwingungen unterschiedlichste, frequenzabhängige Veränderungen der Ausbreitungsgeschwindigkeit.
Für die Anwendung der GPS-Ortungstechnik ist die Kenntnis der unterschiedlichen Phasengeschwindigkeiten von hoher Bedeutung, da die Differenzen bzgl. Geschwindigkeit und Winkel beim Empfang in Entfernungen umgerechnet werden! Nicht rückführbare Abweichungen in den Laufzeiten führen deshalb auch immer zu Ortungsfehlern! Die Kompensation der Brechungsabweichungen wird über mathematische Modelle vollzogen, welche die Effekte der atmosphärische Refraktion minimieren.
Freiraumausbreitung
Nach Mansfeld (1998) stellt für die Betrachtung der Leistungsbilanz einer hochfrequenten Funkverbindung zwischen den Satelliten und einem Meßpunkt auf der Erdoberfläche die Freiraumausbreitung der Welle den wesentlichen Prozeß dar.
Unter Freiraumausbreitung wird die ungestörte Ausbreitung der elektromagnetischen Welle verstanden, d.h. im Ausbreitungsweg darf sich kein Hindernis befinden, welches die freie Ausbreitung beeinträchtigen könnte.
Für Frequenzen oberhalb 300 MHz ist dies immer eine 'quasioptische' Sichtverbindung zum Sender!
Die vom Sender ausgehende Leistung (Ps) wird durch den Einsatz einer Richtantenne um den Antennengewinn (G s) erhöht (Abb. 4.2.1). In der Entfernung des Empfängers (e) kann folgende Leistungsdichte (S ) gemessen werden: S = P s G s / 4 π e 2
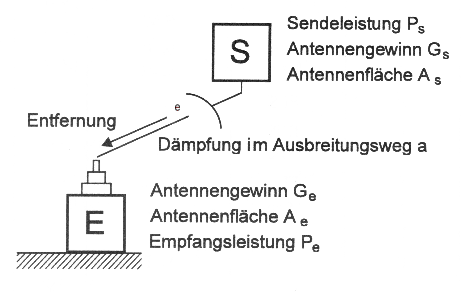
Abb. 4.2.1: Kenngrößen einer Funktverbindung (Mansfeld, 1998)
Der Antennengewinn ist demnach : G = 4 πe A / λ2
Hat die Antenne des Empfängers hat eine Fläche Ae, dann ist die Empfangsleistung Pe : P e = A e S bzw. A e P s G s / 4 πe 2
Wird der Antennengewinn G s durch die Antennenfläche (A) ausgedrückt, gilt: P e = e A e A s f 2 P s / c 2 e 2
Bei konstanter Antennenfläche heißt dies, daß die Empfangsleistung mit dem Quadrat der Frequenz ansteigt!
Die Wirkung beider Antennen kann auch durch ihre Gewinne (G) ausgedrückt werden:
P e = c 2 G e G s P s / (4 π) 2 e f 2 e 2Bei gleichbleibendem Antennengewinn ist die Empfangsleistung also reziprok dem Quadrat der Frequenz! Dies ist für die Frequenz des GPS-Satelliten-Signals wichtig, da die Antennen des Handempfängers im Allgemeinen keine Richtwirkung haben und klein sind, so daß G e = 1 ist! Die Richtwirkung der Sendeantenne im Satelliten ist meist begrenzt auf den Sichtwinkel zur Erdoberfläche. Damit ist auch der Maximalwert des Antennengewinns G s gegeben.
Mit der Wahl einer niedrigen Sendefrequenz ist also eine hohe Empfangsleistung zu erzielen, wenn das Produkt der Antennengewinne vorgegeben ist.
Wird der direkten Funkverbindung Satellit-Empfänger ein Hindernis zugeordnet, also nur eingeschränkte Freiraumbedingungen herrschen, geht die Empfangsleistung stark zurück. Dies gilt auch bei der Verwendung von Frequenzen oberhalb 10 GHz, bei denen die Atmosphäre die ungehinderte Ausbreitung durch Dämpfung behindert (s.u.).
Reflexion
Bei dem Auftreffen einer elektromagnetischen Strahlung auf ein neues physikalisches Medium (also an der Grenze zwischen zwei Medien mit unterschiedlichen elektromagnetischen Eigenschaften) wird immer ein Teil der einfallenden Welle reflektiert, ein weiterer gebrochen (Mansfeld, 1998). Die Unterschiede zwischen den Medien wird durch die Brechzahl n charakterisiert und kann im Unterschied zur Beschreibung mittels Geschwindigkeitsunterschiede (s.o.!) auch über die direkten physikalischen Eigenschaften der Medien beschrieben werden: n = (ε2 μ2 / ε1 μ1 ) 0,5
wobei ε die Dielektrizitätskonstante und μ die Permeablitätskonstante der Medien darstellen.
Fällt eine ebene Welle unter dem Winkel Ψ auf eine Trennfläche, so wird sie z.T. oder auch vollständig unter dem Winkel reflektiert (Abb. 4.2.2). Der restliche Teil dringt in das Medium ein, wobei sie eine Richtungsänderung erfährt, also gebrochen wird. Das Verhältnis der Amplituden des elektrischen Feldvektors der reflektierten Welle zur einfallenden Welle ist die Reflexionszahl. Sie ist abhängig von der Brechzahl, der Frequenz bzw. Wellenlänge, der Polarisation und dem Einfallwinkel der Welle.
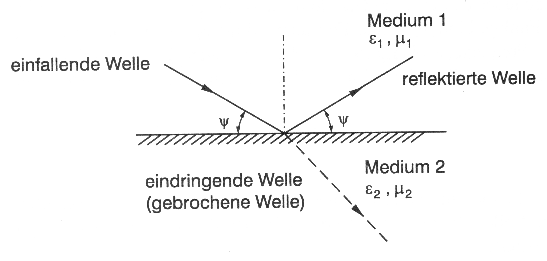
Abb. 4.2.2: Reflexion einer Welle an der Grenzfläche zweier Medien (Mansfeld, 1998)
Auch im GPS treten Reflexionen auf, z.B. wenn der Empfangsort zwischen hohen Gebäuden liegt und/oder kein direkter Sichtkontakt (s.o.) zu den Satelliten besteht (Abb. 4.2.3) . Da das Signal über die Reflexion einen längeren Weg durchlaufen hat, wird auch eine längere Laufzeit und Phasenwinkel somit auch veränderte Entfernungen gemessen, was zu fehlerhaften Positionen führt! Für Mehrfachempfang, d.h. dem gemischten Empfang von direkten und reflektierten Wellen gilt ähnliches. Der Ortungsfehler aufgrund von Mehrwegeausbreitung kann deshalb erheblich sein und tritt überwiegend in dicht bebauten oder bergigen Regionen auf.
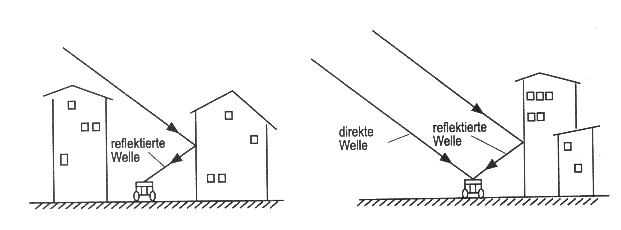
Abb. 4.2.3: Reflexionen beim Empfang von GPS-Satellitensignalen mit Mehrwegeausbreitung (Mansfeld, 1998)
Atmosphärische Brechung (Refraktion)
Da die Erdatmosphäre durch eine schalenförmige Schichtung unterschiedlicher Bereiche mit variierenden (di-) elektrischen Eigenschaften beschrieben werden kann, treten auch hier Refraktionserscheinungen bzgl. der Satellitensignale auf (s.o.). Die atmosphärische Brechung führt auch zu Richtungsänderungen und somit zu veränderten Signallaufzeiten, welche sich auf die GPS-Positionierung auswirken. Diese kann jedoch als relativ klein gegenüber den Veränderungen der Wellengeschwindigkeit ( v ) durch Reflexion angenommen werden.
Für die Brechungseffekte sind vor allem die Troposphären- (0-60 km) und die Ionosphärenschichten (bis 1000 km) verantwortlich. In der Troposphäre spielen sich die Wettererscheinungen ab, welche besonders oberhalb von 10 GHz zu Dämpfungserscheinungen (Energieabsorption) führen. In höheren Schichten nehmen die Feuchtigkeit, die Temperatur und der Druck ab.
Für die Satelitensysteme stellt die Troposphäre ein nicht-dispersives Medium dar, d.h. es ist die Erscheinungen sind bis etwa 10 GHz unabhängig von der Frequenz. Die Phasengeschwindigkeit (vp) und Gruppengeschwindigkeit (vg) zeigen kein unterschiedliches Verhalten in Bezug zur Brechzahl (n).
Mit Hilfe von empirischen Methoden kann die atmosphärische Brechzahl der Troposphäre mit folgender Gleichung annähernd bestimmt werden: n = 1 + 1/10 6 (C 1 P-p/T + C 2 p/T + C 3 p/T 2 )
wobei C 1 bis C 3 Konstanten, P der Luftdruck, p der Partialdruck des Wasserdampfes und T die Temperatur in Kelvin bedeuten.
Nach (Mansfeld, 1998)ist die Berechnung von n längs des Ausbreitungsweges durch Tropos- und Ionosphäre sehr aufwendig und kann aufgrund der fehlenden Detailkenntnisse der einzelnen, stets variierende Parameter zum Messzeitpunkt nur bedingt erfolgen. Vielmehr benutzt man in der Satellitentechnik spezielle mathematische Modelle, welche aufgrund von empirischen Methoden die Brechzahl in Abhängigkeit der Höhe abschätzen können.
Aufgrund der allg. Laufzeitverlängerung sind die ermittelten Positionen dennoch mit zusätzlichen Fehlern behaftet. Dies bedeuted auch, daß der Fehler mit zunehmenden Erhebungswinkel des Satelliten in Bezug zum Beobachtungsort abnimmt (Abb. 4.2.4), da die Laufstrecke in der Atmosphäre auch kürzer wird. Zusätzlich gilt, daß je höher der Wasserdampfgehalt desto niedriger die Brechung, um so kleiner der Entfernungs- und Positionsfehler!
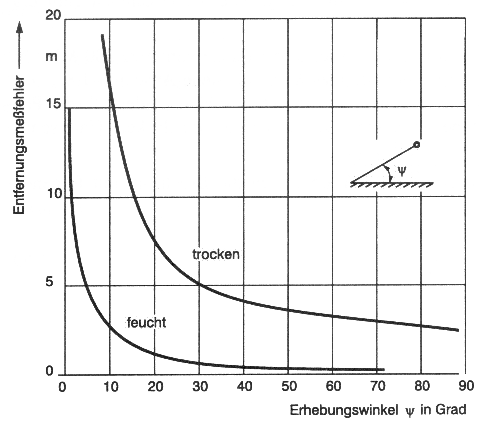
Abb. 4.2.4: GPS-Entfernungsmeßfehler durch troposphärische Brechung in Abhängigkeit des Erhebungswinkels(Mansfeld, 1998)
Die Ionosphäre reicht von ca. 60 km bis in etwa 1000 km Höhe. Die UV-Strahlung der Sonne sorgt hier für die Ionisierung der Moleküle und Atome, wobei unterschiedlich stark gesättigte Zonen innerhalb der Ionosphäre resultieren (ein besonders schönes Phänomen ist das Nord-/Südlicht (Aurora borealis/australis) , welches durch Anregung der elektrisch geladenen Teilchen in nördlichen/südlichen Polarbreiten hervorgerufen wird).
Der Zustand der Ionosphäre wird über die Elektronendichte (Ne) angegeben (Anzahl von Elektronen pro m3). Generell lassen sich fünf Zonen (Schichten) maßgeblicher Elektronendichten abgrenzen:
- D-Schicht (-> 60 km)
- E1-Schicht (-> 100 km)
- E2-Schicht (-> 140 km)
- F1-Schicht (-> 200 km)
- F2-Schicht (200 - 1000 km)
Die Ionosphäre ist ein dispersives Medium, in der die Brechzahl frequenzabhängig ist. Es muß daher zwischen einer Brechzahl bzgl. der hochfrequenten Trägerwelle einer Frequenz (n p ) und der Brechzahl für eine Gruppe von Frequenzen (n g ) unterschieden werden. Es gelten die Beziehungen: n p = C / v p und n g = C / v g
Die Brechzahl n p kann für Kompensationsmodelle auch als Potenzreihe dargestellt werden: n p = 1 + c 2 / f 2 + c 3 / f 3 + c 4 / f 4 + …
Die Koeffizienten c 1 , c 2 …, sind vom momentanen Zustand der Ionosphäre abhängig und damit von der Elektronendichte. In der GPS-Technik gilt folgende Vereinfachung: n p = 1 + c 2 / f 2
Ist die vorhandene Elektronendichte abschätzbar kann die Brechzahl berechnet werden. Auch hier greifen wieder in der GPS-Software vorgehaltene mathemathische, empirische Modelle, deren Ergebnisse in der Praxis ausreichen. Die Brechzahl ist umgekehrt proportional abhängig von dem Quadrat der Frequenz. Die Bestimmung des Koeffizienten c 2 wird durch die gemeinsame Betrachtung zweier verschiedener Frequenzen vom Satelliten aus abgeschätzt (deshalb auch L1 und L2 !).
Empirisch gilt hier c 2 = -40,3 N e
Aus den Zusammenhängen zwischen Phasenlaufzeit v p und Gruppenlaufzeit v g ergibt sich für n g : n g = 1 + 40,3 N e / f 2
Es zeigt sich, daß der Einfluß (Dämpfung/Brechung) der Ionosphäre auf die Phasen- und Gruppenlaufzeit annähernd gleich, aber mit umgekehrten Vorzeichen ist. Durch die Verwendung hoher Frequenzen können die Einflüsse der atmosphärischen Refraktion stark reduziert werden, wobei jedoch bei sehr hohen Frequenzen die zunehmende atmosphärische Dämpfung (s.o.) steigenden Einfluß gewinnt. Die GPS-Frequenzen stellen deshalb einen Kompromiß zwischen geringer atm. Refraktion und steigender atm. Dämpfung dar (vgl. Kap. 2)!
Aus der Kenntnis der Elektronendichte und Brechzahlen läßt sich auch Laufzeit der Wellen experimentell berechnen. Bei Laufzeitabweichungen kann dann auf die Entfernungsmeßfehler zurückgerechnet werden (diese sind deshalb von der Frequenz und der Elektronendichte abhängig). In Abbildung 4.2.5 sind die Entfernungsmeßfehler für zwei unterschiedliche Elektronendichten aufgezeigt.
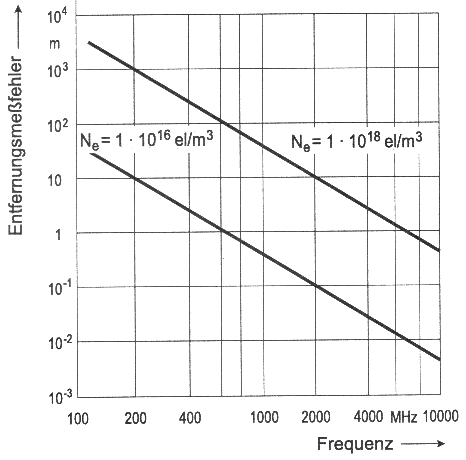
Abb. 4.2.5: GPS-Entfernungsmeßfehler (experimentell) durch ionosphärische Brechung in Abhängigkeit der Frequenz und der Elektronendichte (Mansfeld, 1998)
Atmosphärische Beugung
Elektromagnetische Wellen dringen auch in Schattenbereiche von Hindernissen ein, da sie ähnlich der Lichtwellen gebeugt werden, sofern die Spitze des Hindernisses einen Radius hat, der in der Größenordnung der Wellenlänge oder darunter liegt. Die Wellenlängen innerhalb des GPS liegen unter 1m (L1 = 19,05 cm und L2 = 24,45 cm), so daß der durch die Beugung erfasste Entfernungsbereich mit einem Vielfachen der Wellenlänge relativ klein ist und keine praktische Bedeutung hat. Auf jedem Fall wird durch Beugungserscheinungen eine Wegstrecke zusätzlich verlängert, was in Extremfällen unmittelbar zu Ortungsfehlern führen kann.
Atmosphärische Absorption
Energieanteile der elektromagnetsiche Wellen werden unter bestimmten Bedingungen in der Atmosphäre absorbiert. Der Energieverlust wird auch als Ausbreitungsdämpfung bezeichnet (a ). Sie ist das Verhältnis der Eingangsleistung P 1 zu Ausgangsleistung P 2 und wird durch den zehnfachen Logarithmus zur Basis 10 angegeben. Ihre Maßeinheit ist Dezibel (dB): a = 10 lg P 1 / P 2
Besondere Faktoren hoher Absorption sind
- endliche Leitfähigkeit des Erdbodens
- dielektrische Verluste in Niederschlagspartikeln
- molekulare Resonanzabsorption
Für die GPS-Meßtechnik sind besonders Absorptionen durch Regen, Nebel oder Schnee von Bedeutung. Sie sind die wesentlichen Faktoren der atmosphärischen Absorption (Tab. 4.2.1).
Tab. 4.2.1 Dämpfung in dB/km durch atmosphärische Niederschläge (Mansfeld, 1998)
| Regen: | Frequenz: | ||||
| Art | Intensität | 450 MHz | 1 GHz | 3 GHz | 10 GHZ |
| Sprühregen | 0,25 mm/h | 2,2 x 10 -8 | 1,5 x 10 -6 | 1,5 x 10 -4 | 0,22 |
| leichter Regen | 5 mm/h | 1,0 x 10 -6 | 2,0 x 10 -5 | 1,0 x 10 -3 | 0,08 |
| mäßiger Regen | 12,5 mm/h | 3,0 x 10 -6 | 7,0 x 10 -5 | 3,0 x 10 -3 | 0,28 |
| starker Regen | 25 mm/h | 7,5 x 10 -6 | 1,5 x 10 -4 | 1,0 x 10 -2 | 0,60 |
| Schauer | 50 mm/h | 1,0 x 10 -5 | 3,0 x 10 -4 | 2,0 x 10 -2 | 1,5 |
Die horizontale Ausbreitung eines Regengebietes ist meist umso weiter, je geringer die Niederschlagsintensität ist. Bei heftigen Regengüssen ist die vertikale Ausdehnung relativ weit, da sich große Tropfen nur in großer Höhe und bei niedrigen Temperaturen bilden. Berücksichtigt man die Ausdehnung eines Regengebietes, wird deutlich, daß der Erhebungswinkel einer Verbindungslinie Satellit-GPS-Empfänger für den Dämpfungsumfang wichtig ist. Bei geringen Erhebungswinkeln ist der Signalweg länger, die Dämpfung also höher!
Nebel und Schnee verursachen Ausbreitungsdämpfungen vergleichbar denen des Regens, wenn die Wassermenge pro Volumeneinheit etwa gleich ist. So lassen sich bzgl. der Dämpfung von Nebel mit einer Sichtweite unter 100 m mit Regenschauern einer Intensität von 1mm/h vergleichen!
Die Dämpfung verursacht durch molekulare Absorption tritt immer und zusätzlich auf! Verantworlich sind Schwingungen des Wassers und des Sauerstoffs in der Atmosphäre, wobei Maximalwerte genau im Resonanzfall der Molekülschwingung auftreten (Tab. 4.2.2). Oberhalb von 10 GHz können die Dämpfungseffekte so hoch werden (Abb. 4.2.6), daß Funkverbindungen erheblich gestört wären. Der Sauerstoffgehalt nimmt mit der Höhe stark ab (> 100 km fast bei 0), das Gleiche gilt für Wasserdampf (>10 km), so daß die Dämpfungswerte nicht nur frequenzabhängig, sondern auch abhängig von der Höhe sind!
Tab. 4.2.2 Dämpfung in dB/km durch atmosphärische Molekular-Resonanz (Mansfeld, 1998)
| Resonanzfrequenz (GHz) | Moleküle | Dämpfung (dB) |
| 22,2 | H 2 O | 0,15 |
| 60 | O 2 | 14 |
| 118 | O 2 | 2,1 |
| 183 | H 2 O | 28 |
| 320 | H 2 O | 20 |
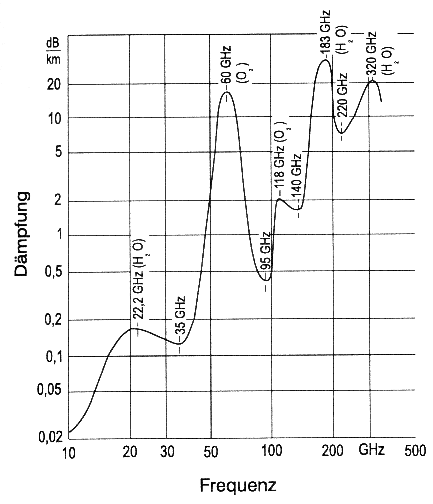
Abb. 4.2.6: Dämpfung in dB/km durch atmosphärische Molekular-Resonanz (Mansfeld, 1998)
Atmosphärische Streuung
Genau wie optische Strahlen werden elektromagnetische Funkwellen an Partikeln gestreut, wenn deren Ausmaße groß im Verhältnis zur Wellenlänge sind. Die Streuung an Inhomogenitäten in der Atmosphäre bewirkt eine diffuse Ablenkung der Strahlung aus ihrer ursprünglichen Ausbreitungsrichtung heraus. Insbesondere Makrostrukturen wie Turbulenzen führen bei Funkwellen unter geringem Ausbreitungswinkel zu starken Streuungseffekten. Da während der GPS-Messung eine quasioptische Verbindung zum Satelliten bestehen sollte, treten Streuungseffekte aufgrund von Turbulenzen nicht auf (Horizontalwinkel > 10°). Negative Einflüsse aufgrund von Partikelstreuung wird über die Implementierung mathematischer Modelle begegnet.
