Messung und Datenverarbeitung

5.1 Auswerteverfahren

Das GPS beruht auf einem wesentlichen Grundprinzip der Satellitengeodäsie (Brinkkötter-Runde, 1995) , nämlich dem Einweg-Entfernungsmeßverfahren. Vier Parameter spielen hier eine grundsätzliche Rolle (je nach GPS-Typ):

Pseudoentfernungsmessungen aus Code-Messungen
Pseudoentfernungsdifferenzen aus intergriertem Doppler-Count
Signallaufzeitdifferenzen aus interferometrischen Messungen
Trägerphasendifferenzen der Wellen

Bedeutung für die Praxis

In der Praxis werden in erster Linie Messungen der Laufzeiten von Codes und Verschiebungen in der Trägerphase von vier Satelliten gemessen, welche beide von der relativen Entfernung zwischen dem Empfänger und den Satelliten bzw. anderer Einflußgrößen (s.o.) abhängen (Abb. 5.1.1) . Die errechnete Laufzeit eines Signals von der Satelliten- zur Empfangsantenne wird so in eine Entfernung umgewandelt.

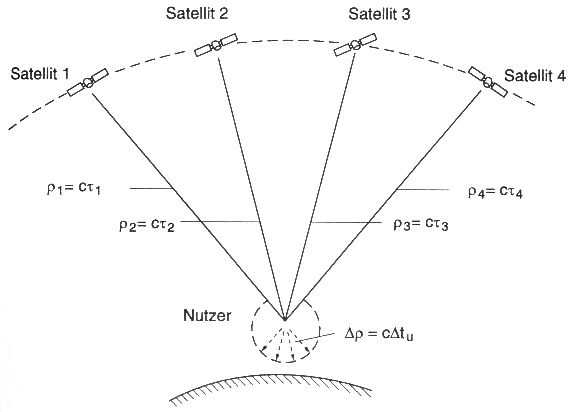
Abb. 5.1.1: Schematische Darstellung der GPS-Satellitenortung (Rho und Tau sind entspr. Phasenwinkel- und Zeitversätze) (Mansfeld, 1998)

Bei sehr genauen Meßanforderungen wird die Entfernung nicht nur über die Messung der Laufzeiten bestimmt (Impulsmeßverfahren), sondern über die alleinige Trägerphasenwinkelabweichungen der hochfrequenten Signale. Letztere Messung erfordert mehr Zeit und ist deshalb als sog. CW-Verfahren nur für die Geodäsie (Dauermessung) von Relevanz (vgl. Kap. 5.2) .

Für Ortungsverfahren schnell bewegter Objekte mittels GPS wird das Impulsmeßverfahren angewandt, welches über eine Zeitsynchronisation zwischen Empfänger und Sender die aus Phasenwinkelverschiebungen ermittelten Laufzeiten der Code-Information mit einem identisch generierten Signal im Empfänger vergleicht. Die Zeitverschiebung δt ist nur näherungsweise gleich dem geometrischen Abstand (ρ, über Phasenwinkel) zwischen Satelliten und Empfänger, da die Uhrzeiten beider Komponenten streng genommen unterschiedlich sind. Die ermittelten Entfernungen werden deshalb Pseudoentfernungen oder Pseudoranges genannt.

Pseudoentfernungen

Pseudoentfernungen werden in der GPS-Technik über Kreuzrelationen ermittelt (Abb. 5.1.2). Wie in Kapitel 2.3 bereits erläutert, wird die Trägerfrequenz des C/A-Codes mit einer Pseudo-Zufallsfolge moduliert, um eine Phasenmehrdeutigkeit auszuschließen. Der aufmodulierte Code besteht aus 1023 Bit, die periodisch mit einer Grundfrequenz von 1,023 MHz übertragen werden. Der Code wiederholt sich somit jede Millisekunde, was bei einer Umlaufhöhe der Satelliten von ca. 20.200 km und der ungehinderten Ausbreitung vorausgesetzt (c = 300.000 km/s) in einer Laufzeit für das Signal von etwa δt = 0,07 s zum Empfänger münden würden. Es gilt: δt = ρ / c

Für den im Empfänger erzeugten Signalcode heißt dies, daß er gegenüber dem Satelliten-Code um ca. 70 ms verschoben ist. Die Entfernung und die exakte Laufzeit kann somit auch über einen direkten Vergleich der Codes über eine Summenbildung der Phasenverschiebung ermittelt werden.

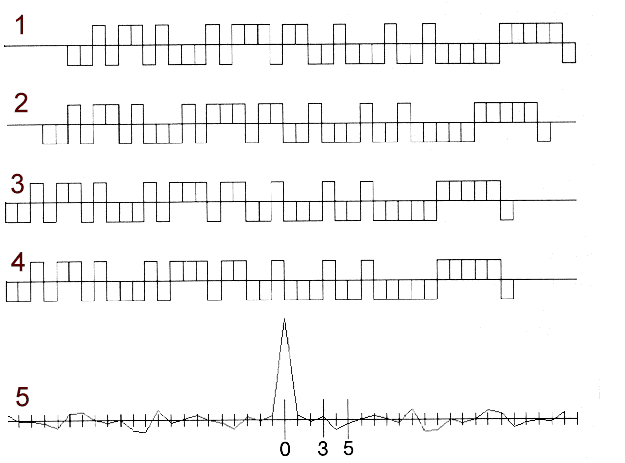
Abb. 5.1.2: Schematische Darstellung verschobener GPS-Codes und der Korrelationsfunktion; 1 = Satellitencode, 2 = Satellitencode 2Ms versch., 3 = Satellitencode 5Ms versch., 4 = Empfängercode und 5 = Korrelationsfunktion (Kumm, 1997)

Um das Satellitensignal im Empfänger abbilden zu können, muß der PRN-Code bekannt sein. Multipliziert und summiert man nun empfangenes und rekonstruiertes Signal miteinander, liegt als Ergebnis eine Korrelationsfunktion vor. Die zur Modulation der GPS-Signale gewählten PRN-Codes bewirken, daß die Korrelationsfunktion nur dann den Wert +1 annimmt (also positiv redundant sind), wenn Frequenz, Träger und Code-Phase der korrelierten Signale exakt übereinstimmen.

Das Prinzip:
Vom Satelliten geht das Signal f 1 aus, welches vom Empfänger auch durch Doppler-Effekte verschoben empfangen wird (f e ), da sich sowohl Satellit als auch Empfänger durch die Erdrotation bewegen. Durch den in Frequenz und Phase nachsteuerbaren Empfänger-Oszillator wird die Frequenz f i erzeugt, die solange geändert wird bis f i = f e ist (Abb. 5.1.3). Ist dieser Zustand einmal erreicht, wird die Synchronisation der Frequenzen für die gesamte Zeitspanne der Satelliten-Sichtbarkeit beibehalten.

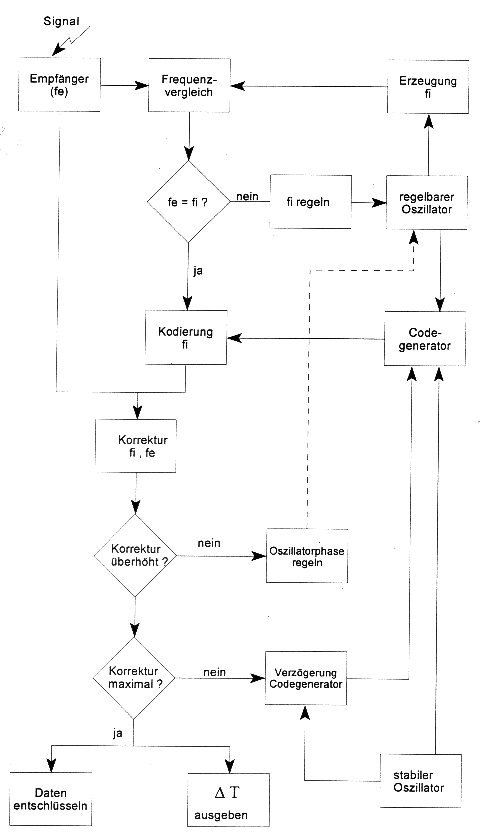
Abb. 5.1.3: Schematischer Ablauf der Code-Synchronisation und Zeitdifferenzberechnung (Brinkkötter-Runde, 1995)

Ist die Bedingung der Frequenzgleichheit einmal gegeben, wird die intern erzeugte Frequenz f i mit der Satelliten-identischen PRN-Sequenz über einen Codegenerator kodiert, der seinen Takt von einem nachsteuernden Oszillator erhält. Es liegt also nun ein Duplikat des empfangenen Satellitensignals vor, welches allerdings keine Dateninformation enthält. Dublikat und Originalsignal werden nun korreliert. Voraussetzung für eine leichte aber signifikante Überhöhung der Korrelationsfunktion ist die Tatsache, daß Satelliten- und Empfängersignal nicht nur in der Frequenz, sondern auch in der Phase übereinstimmen müssen. Es muß somit auch die Phase des Klons stufenweise nachgeregelt werden, bis durch die Überhöhung der Funktion beide Signale auch in der Phase übereinstimmen.

Ausgangspunkt ist die Austrahlung des Satellitensignals T 0 , welches nach ca. 70 Ms den Empfänger erreicht und dort mit dem zeitgleich erzeugten Signal verglichen wird. Der genaue Zeitversatz wird anhand der schrittweisen Verzögerung des Code-Generators ermittelt. Bei völliger Synchronisation liegen für alle resultierenden Amplitudenfunktionen nur +1-Werte in der Kreuzrelation vor. Die letztlich erreichte Phasenverschiebung (Codephase) ist ein Maß für die tatsächlich aufgetretene Laufzeit δT des Satellitensignals. Dieser Zeitversatz wird nun immer durch Nachsteuerung des Code-Generators vorgehalten. Multipliziert man nun das empfangene Signal mit dem phasenrichtigen Klon erhält man als Resultierende den reinen Datencode!

Da Satelliten- und Empfangsuhr jedoch nicht wirklich übereinstimmen und die Geschwindigkeit des Signals aufgrund unterschiedlichster Effekte nicht gleich der Lichtgeschwindigkeit ist, bildet das Produkt aus δ T c nur die Pseudoentfernung ab (Abb. 5.1.4)!

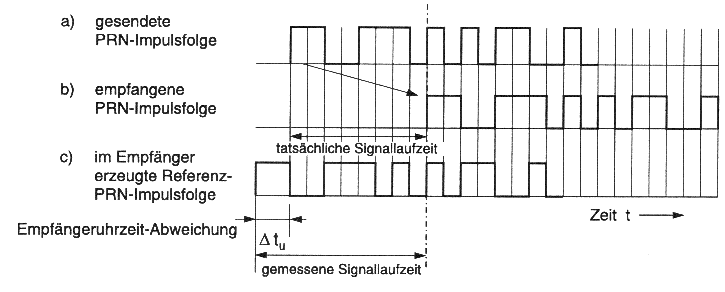
Abb. 5.1.4: Korrelationsprozeß bzgl. des PRN-Codes im GPS-Empfänger (Mansfeld, 1995)

Um in der Praxis die Uhrenfehler reduzieren zu können, werden leistungsstarker GPS-Empfänger mit einer korregierenden Zeitkonstante, dem sog. Empfängeruhrenfehler (u) beschickt. Die tatsächliche Laufzeit erhält man, indem mittels Kreuzrelation bestimmte Verzögerungen (vgl. Kap. 4) um u korrigiert werden. Die Strecke ρ ist dann gleich: (δT + u) c = ρ

Die tatsächliche Distanz wird im Praxisfall über fortlaufende Iterationsschritte ermittelt. Beträgt die der wirkliche Zeitversatz z.B. 5 Ms, entspräche dies gerade einer Wegstrecke von ca. 1,5 km! Da der vollständige C/A-Code bei 1000 Sekunden Sendedauer jedoch 300 km lang ist, ist es nur möglich innerhalb dieser 300 km eine Distanz zur berechnen. Der GPS-Empfänger geht deshalb immer von einer Grundentfernung (berechnet aus den 7 Ms Mindestlaufzeit) aus, zu der dann die tatsächliche Streckendifferenz hinzugerechnet wird. Die Entfernung kann in unserem Beispiel also nur zwischen 21.000 und 21.300 km liegen; hier sind es 21.000 km + 1,5 km = 21.001,5 km! Da die Verschiebung des Empfängercodes in Relation zum Sendercode bis auf 1% eines Bit erfolgt und dieses Bit etwa eine Ms oder 300 m lang sein kann, ist die ermittelte Entfernung auf ca. 3 m genau. Doch hierzu im nächsten Kapitel mehr …