3.2 Frequenz- und Zeitnormale
Frequenz und Zeit sind gesetzmäßig miteinander verknüpft
(Mansfeld, 1998) , da die Frequenz per Definition die Anzahl von Ereignissen pro Zeitintervall
widerspiegelt (z.B. Anzahl der Schwingungen pro Sekunde). Zeitnormalen sind hochgenaue Uhren, deren
Wirkungsprinzip auf eine Frequenznormale zurückzuführen sind. Durch Teilung der von einem Frequenznormal
erzeugten Frequenz werden die zur Umsetzung einer Zeitskala nötigen Intervalle genommen.
Diese Zeitskalen weisen gegenüber der idealen Zeitskala geringe Abweichungen auf, deren Ursachen gegeben
sind durch:
- interne Abweichungen der Frequenz (Offset)
- Abweichungen der Frequenz durch klimatische Einflüsse (Temperatur, Luftdruck..)
- Frequenzdrift durch Alterung der Wellen
- Schwankungen in der statistischen Verteilung
Man unterscheidet zwei Frequenznormalen, welche in der Zeitnormale zum Einsatz kommen:
- Quarzoszillatoren
- Atomfrequenznormale
Beide finden in der GPS-Technik Anwendung und sind deshalb von Bedeutung!
Quarzoszillatoren
Der Quarzoszillator ist ein elektrischer Schwingungserzeuger, welcher im positiven Rückkopplungszweig einen Quarzresonator als frequenzabhängiges Element enthält, der aus einem natürlichen oder künstlichen Quarzkristall besteht (SiO 2 ). Er besitzt eine hohe Frequenzselektivität, die durch die sog. Resonatorgüte definiert wird, welche wiederum abhängig vom Kristallschnitt, der Kristallgröße und den äußeren Einflüssen (Temperatur, Luftfeuchte...) ist. Auch das Kristallalter spielt eine (allerdings untergeordnete) Rolle für die Resonanzfrequenz.
In der Praxis unterscheidet man zwischen:
- einfachen Quarzoszillatoren, oft als Taktoszillatoren bezeichnet
- temperaturkompensierten Oszillatoren (TCXO, wobei X = Kristall)
- thermostatisierte Oszillatoren (Oven Controlled Crystal Oscillators = OCXO)
Da die Temperatur der Oszillatorumgebung hauptsächlich die Stabilität der Frequenz beeinflußt, werden durch elektronische Schaltungen ein Teil der temperaturabhängigen Schwankungen kompensiert. Darüber hinaus wird eine Stabilisierung der Frequenz über den Einbau eines Thermostaten geregelt (Temperaturkonstanz von etwa +/- 0,01°C), so daß die verbleibende Frequenzänderung gering ist (vgl. Tab. 3.2.1).
Tab 3.2.1: Kennwerte von Quarzoszillatoren mit Thermostaten (OCXO) nach Mansfeld, (1998)
| Parameter | kommerzielle Ausführung | experimentelle Ausführung |
| Frequenzinstabilität bei t = 1s | 10 -10 bis 10 -12 | 2 x 10 -13 |
| Frequenzflickern bei t > 1s | 10 -11 bis 10 -12 | 10 -13 |
| Frequenzdrift pro Monat | 10 -7 bis 5 x 10 -9 | 3 x 10 -10 |
| Temperatureinfluß pro 1 K | 10 -9 bis 10 -11 | 10 -12 |
Wegen der niedrigen Gerätekosten und der einfachen Betriebsweise (Ökonomie) finden Quarzoszillatoren in GPS-Empfängern Einsatz. Darüber hinaus sind Quarzoszillatoren in den Atomfrequenznormalen als Sekundärnormale enthalten, wobei eine laufende Nachsteuerung der Frequenznormalen erfolgt. Sie sind somit Bestandteil der ortungstechnischen Einrichtungen der Satelliten (Mansfeld, 1998).
Atomfrequenznormale
In den Atomuhren werden Eigenschaften einzelner freier Atome zur Erzeugung von Schwingungen genutzt, welche eine zeitlich unveränderbare Referenzfrequenz liefern. In einem Atom können die Elektronen nur ganz bestimmte Energiezustände einnehmen, so daß ein Wechsel des Zustandsniveaus von E 2 nach E1 (unter der Bedingung von E2> E1) stets mit einer Energiefreisetzung in Form von elektromagnetischer Strahlung verbunden ist.
Ihre Frequenz ist wie folgt: f = (E 2 - E 1 ) / h (wobei h = Planck'sches Wirkungsquantum )
Für Atomuhren sind Übergänge zwischen Energieniveaus besonders geeignet, wenn für diese eine besonders lange natürliche Lebensdauer gilt. Die Resonanzfrequenz muß leicht meßbar und synthetisierbar sein, da mit ihr ein OCXO nachgeregelt wird, d.h. die Schwankungen der Resonanzfrequenz des OCXO wird durch die Resonanzfrequenz der Atomnormale ersetzt bzw. eleminiert.
Rubidium-Uhren (-normalen)
Eine häufig verwandte Atomuhr ist die Rubidium-Frequenznormale (Rb-Uhr), welche auf dem Übergang zwischen dem Energieniveau von 87 Rb aus dem Grundzustand der Hyperfeinstruktur basiert. Die Frequenz der Strahlung ist:
f Rb = (E 2 - E 1 ) / h = 6,834682613 GHzRb-Uhren sind für unterschiedlichste Aufgaben mit verschiedenen Betriebseigenschaften verfügbar, je nachdem welche Baugrößen und Funktionalitäten gewünscht wird.
Cäsium-Uhren (-normalen)
Eine weitere häufig verwandte Atomuhr ist die Cäsium-Frequenznormale (Cs-Uhr), welche auf dem Übergang zwischen dem Energieniveau von 133Cs aus dem Grundzustand der Hyperfeinstruktur basiert. Die Frequenz der Strahlung ist:
f Cs = (E 2 - E 1 ) / h = 9,192631770 GHzCs-Uhren sind für unterschiedlichste Aufgaben mit verschiedenen Betriebseigenschaften verfügbar, je nachdem welche Baugrößen und Funktionalitäten gewünscht wird (vgl. auch Tab. 3.2.2).
Tab 3.2.2: Kennwerte der Rb- (a) und Cs-Frequenznormalen (b) in entsprechenden Atomuhren
| a) Parameter Rb-Uhr | kommerzielle Ausführung | GPS-Satelliten |
| Frequenzinstabilität bei 1s < t < 100s | 2 x 10 -11 | 3 x 10 -12 |
| Frequenzflickern bei t > 1000s | 5 x 10 -13 | 10 -14 |
| Frequenzdrift pro Monat | 4 x 10 -11 | 2 x 10 -12 |
| Temperatureinfluß pro 1 K | 3 ... 10 x 10 -12 | 10 -13 |
| b) Parameter Cs-Uhr | kommerzielle Ausführung | CS-2, experim. Ausf. Braunschweig |
| Frequenzinstabilität bei 10s < t < 10 4 s | 10 -11 | 3,5 x 10 -12 |
| Frequenzunsicherheit | 7 x 10 -12 | 1,5 x 10 -14 |
| Frequenzflickern (24 h/Jahr) | 10 -13 | 10 -15 |
| Frequenzdrift pro Monat | 10 -13 | nicht relevant |
| Temperatureinfluß pro 1 K | 10 -13 | 10 -15 |
Neben den Rb- und Cs- Uhren findet auch das sog. Wasserstoff-Maser-Frequenznormal (H-Maser) in der
Zeitmessung, zumindest in stationären Spezialvorhaben Einsatz. Da es aber nur mit einem relativ hohen
technischen Aufwand zu betreiben ist, wird es in der GPS-Technologie nicht berücksichtigt (fH =
1,420405751 GHz).
Praxisbezug der Frequenznormalen
Abbildung 3.2.1 zeigt die Frequenzinstabilität der einzelnen Strukturen in Abhängigkeit von dem Beobachtungszeitraum.
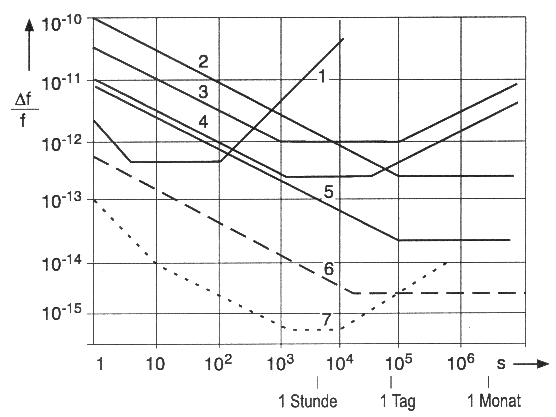
Abb. 3.2.1: Frequenzinstabilitäten (Δ="18">f/f) von Frequenz- und Zeitbasen in Abhängigkeit von der Beobachtungsdauer (Mansfeld, 1998) . 1 = Quarzoszillator, 2 = Cs (standard), 3 = Rb (standard), 4 = Rb (best), 5 = Cs (best), 6 = Cs (exp.) und 7 = H-Maser
Sehr hohe Anforderungen werden an die Frequenz- und Zeitstabilität der Normalen innerhalb der Satellitenortungssysteme gestellt, da hier Laufzeiten von Signalen im Bereich der Lichtgeschwindigkeit und damit Entfernungen gemessen werden. Diese Forderungen lassen sich nur mittels Atomfrequenznormalen erfüllen. Grundsätzlich werden im stationären Betrieb Cs-Uhren eingesetzt, da sie aus unterschiedlichen technischen Gründen hinsichtlich Sicherheit und Stabilität der Frequenz allgemein von Vorteil sind. In Satelliten kommen jedoch Rb-Uhren zum Einsatz, da sie im mobilen Status die beste Kurzzeitstabilität aufweisen. Zur Gewährleistung ihrer Langzeitstabilität wird zusätzlich eine andere Zeitnormale unterstützend herangezogen, beispielsweise Signale von Normalzeitsendern. In Tabelle 3.2.3 sind die Akkumulationswerte der verschiedenen Frequenznormalen zusammengefaßt.
Tab. 3.2.3: Instabilität und Akkumulation von Zeitfehlern bei verschiedenen Frequenznormalen (Mansfeld, 1998)
| Typ | Frequenz (GHz) | Instabilität pro Tag | Verlust von 1s in… |
| Quarz | 0,05 | 10 -9 | 30 a |
| Rb | 6,834682613 | 10 -12 | 30.000 a |
| Cs | 9,192631770 | 10 -13 | 300.000 a |
| H-Maser | 1,420405751 | 10 -15 | 30.000.000 a |
