1.2 Globale Vermessung
Optisch globale Triangulation
Mit dem BC-4 Kamerasystem wurde zum ersten Mal der Versuch unternommen, astronomisch gestützte Positionsbestimmungen mit weltweiter Gültigkeit mittels künstlicher Erdtrabanten zu erlangen. Dazu wurden hoch reflektierende Satelliten mit sogenannten 'Verfolgungs-' oder 'Spurkameras' (tracking cameras) am nächtlichen Firmament in bestimmten Zeitintervallen photographiert (vgl. Kap.1.1). Die Orbitdaten der Satelliten müssen dazu exakt bekannt sein. Mittels photogrammetrischer Methoden wurden dann die astronomischen Koordinaten ausgewählter Sterne und die der Satelliten berechnet bzw. in Bezug zum jeweiligen Beobachtungsort gesetzt. Verglich man nun die zeitgleichen Aufnahmen der Satelliten und der Sternenbahnen mit zeitgleichen Aufnahmen anderer Basispunkte (meist mehrere 1000 km voneinander entfernt!) ließ sich eine gemeinsame Raumrichtung zwischen den Beobachtungspunkten errechnen. Derartige Basisrichtungen wurden dann global aufgespannt und bildeten ein weltweites Netz von Traversen.
Das Hauptproblem dieses Verfahrens war neben seiner Statik und Umständlichkeit die wechselnde Wetterlage: Bei nächtlicher Bewölkung ließen sich keine gemeinsamen Meßstrecken aufspannen, so daß optisch globale Triangulationen sehr schnell durch wetterunabhängige, elektromagnetische Techniken zur astronomischen Positionsbestimmung ersetzt wurden. Zudem lag die Genauigkeit des Verfahrens aufgrund photo-optischer Mängel (z.B. Lichtbrechung in der Atmosphäre) bei nur etwa 5 m. Optische Systeme spielen heute noch eine Rolle in der astronomischen Vermessung von Satellitenbahnen.
Neben der allgemeinen Satellitenphotographie fanden besonders C- und S-Band Radar, GRARR (Goddard Range and Range Rate), SECOR (Sequential collation of range) und Minitrack ihren Einsatz (s.u.). Einige wichtige optische Systeme werden mit ihren technischen Parametern in Tabelle 1.2.1 skizziert.
Parameter wichtiger Instrumente zur optischen Astro-Triangulation
(Wells, 1987)| Instrument | Brennweite | Zeitempfindlichkeit | Richtungsgenauigkeit | Lichtstärke |
| BN-Kamera | 50 cm | 0,1 msek | 2 bsek | 12 |
| Hewitt-Kamera | 63 cm | 0,2 msek | 1 bsek | 7,5 |
| BC-4 Kamera | 12 cm | 0,1 msek | 2 bsek | 6 |
| PC-1000-Kamera | 20 cm | 0,1 msek | 2 bsek | 6 |
| NAFA 3c/25 | 10 cm | 2 msek | 5 bsek | 4,5 |
| MOTS-40 | 20 cm | 2 msek | 2 bsek | 5 |
| Kinetheodolit | 20 cm | 10 msek | 4 bsek | 4 |
| 70-mm Theodolit | 7 cm | 100 msek | 110 bsek | 8 |
| 7 x 50 Fernglas | 5 cm | 100 msek | 110 bsek | 8 |
| 11 x 80 Fernglas | 8 cm | 100 msek | 70 bsek | 9,5 |
| 20-cm Telescope | 20 cm | 100 msek | 70 bsek | 11 |
Elektromagnetische globale Trilateration
Die Wetterabhängigkeit und die schwankende Genauigkeit der weltweit einsetzbaren optischen Triangulation mittels der BC-4 Kamera u.a. optischer Techniken veranlaßte die Wissenschaft und das Militär nach günstigeren Lösungen zur weltweiten Positionsbestimmung zu suchen. Besonders während des Zweiten Weltkrieges war es wichtig global einsetzbare Positionierungverfahren zu optimieren, um so aliierte Flugzeuge sicher im Luftraum Europas zu bewegen. Erstmalig wurden so Radiowellen zur Trilateration (Überlagerung) herangezogen. Das System HIRAN stellte 1940 einen ersten Prototyp zur teilglobalen Positionsbestimmung mittels Radiowellen (Mikrowellen) dar (Hofmann-Wellenhof et al., 1992).
Nach dem Krieg setzte man zunächst weiter auf Radarsysteme, welche im Mikrowellenbereich Signale in Richtung spezieller Reflexionssatelliten aussandten und die Laufzeit-Veränderung des zurückkommenden Signals (Dopplereffekt in Abhängigkeit zum Geoid) in Positionen umrechneten (Wells, 1987). Meist waren dies S- oder C-Band-Radarsysteme militärischer Einrichtungen. Einige wichtige Systeme hießen GRARR, Prime Minitrack oder SECOR. Diese Systeme zeigten im Prinzip eine gleichartige Funktionalität:
Ein Mikrowellen- (Radar-) sender strahlte ein in bestimmten Frequenzbändern moduliertes Signal in Richtung der Satelliten aus, welche dieses Signal an die (z.T. mobilen) Bodenstationen zurücksandten. Die aus den Laufzeitunterschieden resultierende Phasenveränderung (Dopplereffekt) wurde zur Berechnung der Form des Geoides am Beobachtungspunkt und zur Positionierung genutzt (Genauigkeiten lagen zwischen 3 und 10 m).
Mit Beginn der 60'er Jahre wurde an der John Hopkins University das US Navy Navigation Satellite System (NNSS) entwickelt, welches später in TRANSIT umbenannt wurde. Es stellt den eigentlichen Vorläufer des GPS-Positionierungssystems dar und war bis Ende der 80'er Jahre im militärischen, bzw. seit 1967 z.T. auch pilothaft im zivilen Einsatz (Abb. 1.2.2).
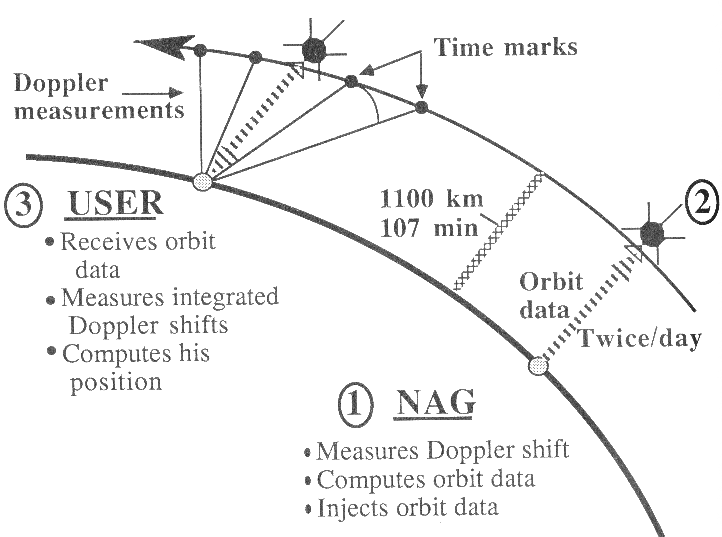
Abb. 1.2.2: Prinzip der TRANSIT (NNSS) Positionierungseinheiten (Wells, 1987)
Das TRANSIT-System bestand aus sechs Satelliten mit polarem Orbit in einer Höhe von ca. 1.100 km
bei einer Umlaufzeit von je 107 Minuten. Die Satelliten wurden von der US Naval Astronomical Group (NAG)
gesteuert und von vier Stationen innerhalb der USA verfolgt. Zweimal am Tag wurden die Dopplermessungen mit den
Ephemeriden (Bahnparameter!) der Satellitenbahnen verrechnet und zu den Satelliten zurückgesandt,
welche dann diese Informationen zu den jeweiligen (mobilen) Empfängern weitergaben. Der Vergleich der empfangenen
Signale mit der geeichten Ozillationsfrequenz der Geländeempfänger (Dopplereffekt, Frequenzverschiebungen)
konnte bei ausreichender Meßdauer (einige Minuten!) eine bis auf 1m genaue Position liefern.
Parallel zu TRANSIT entwickelte die ehem. Soviet Union das vergleichbare System TSICADA. Die
Erfahrungen aus TRANSIT flossen später in das System NAVSTAR/GPS (s.u.) ein
Warum Global Positioning System (GPS)?
Das Global Positioning System (GPS) wurde mit dem Zweck entwickelt, die Nachteile des älteren TRANSIT-Systems zu beseitigen. TRANSIT läßt nur exakte Messungen über eine relativ lange Meßdauer zu, wobei die Satellitenabdeckung global als sehr schlecht galt (nur sechs Satelliten!). Im Durchschnitt konnte innerhalb der USA nur alle 90 Minuten eine günstige Satellitenkonstallation für TRANSIT abgegriffen werden; für alle anderen Zwischenzeiträume mußte die Position interpoliert werden. Im Gegensatz hierzu bietet GPS zum heutigen Zeitpunkt sofort eine Antwort auf die Fragen:
- Wo genau bin ich (3D)?
- Mit welcher Geschwindigkeit bewege ich mich?
- Welche Zeit benötige ich (Uhrzeit) u.v.m.?
Zusätzlich ist die heutige GPS-Technik schnell, hinreichend genau und überall vergleichsweise preiswert für Jede/n nutzbar (Remondi, 1991c).
Das Global Positioning System i.e.S. ging aus dem prototypischen Vorläufer NAVSTAR (NAVigation Satellite Time And Range) Global Positioning System 1973 hervor. NAVSTAR selber war ein aus den Projekten TIMATION (US Navy) und 621-B (US Airforce) unter Berücksichtigung von TRANSIT zusammengeführtes Projekt mit dem Ziel, zunächst eine militärisch nutzbaren Echtzeit-Positionierung sich schnell bewegender Fahrzeuge zu Wasser, zu Lande und in der Luft zu ermöglichen.
Der erste GPS-Satellit (Block I Satellit) wurde am 27. Juni 1977 in sein ca. 20.000 km hohes Orbit um die Erde gebracht. Ihm folgten bis 1990 23 weitere Satelliten um so die globale Abdeckung zu gewährleisten. 1996 waren es bereits 26 operationelle Satelliten (plus Reserve!), heute sind es 32 ( inkl. Reserve), so daß die Verfügbarkeit und Qualität der GPS-Messungen global im Normalfall wenig zu wünschen übrig läßt.
Das GPS besteht prinzipiell aus drei Komponenten (vgl. Abb. 1.2.3):
- GPS-Kontroll System
- GPS-Satelliten
- GPS-Empfänger
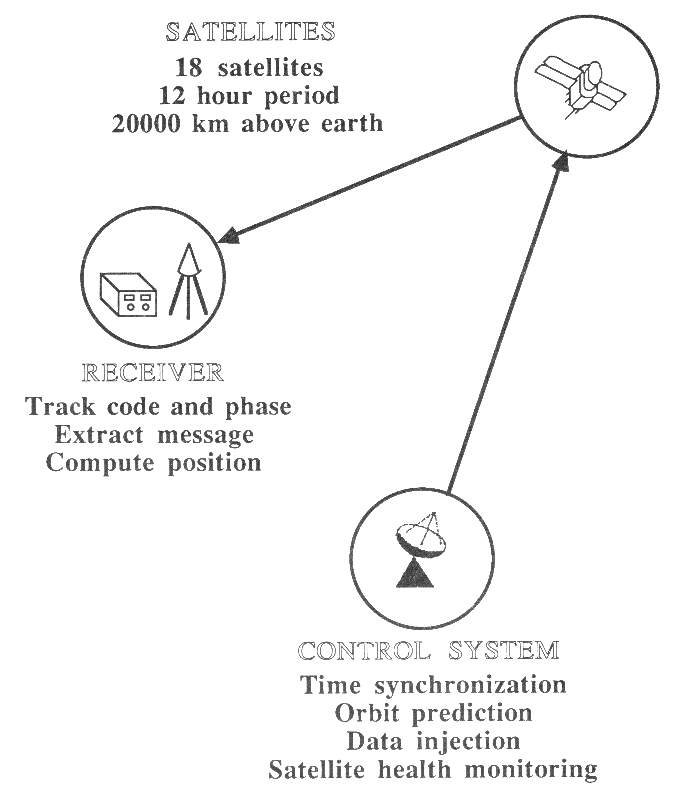
Abb. 1.2.3: Komponenten des Global Positioning Systems GPS (Wells, 1987)
Parallel zur Umsetzung des GPS-Konzeptes machte auch die Computertechnik sehr rasche Fortschritte, so daß eine exakte Echtzeit-Positionierung mittels ausreichend vieler und technisch optimal ausgestatteter Satelliten bzw. qualitativ hochwertiger Empfänger seit den 90'er Jahre erfolgreich umgesetzt wurde. Die Kosten für das ursprünglich rein militärisch ausgelegte GPS waren allerdings enorm hoch (mehr als 10 Mrd. $US !!), so daß man sich rasch hinsichtlich einer zivilen Nutzung kooperativ zeigte.
Neben einem für rein militärische Zwecke reservierten Präzisionssignal (P-Code) wurde ein weiteres 'ungenaues' Signal (C/A-Code) für zivile Zwecke geschaltet, welches von jedem privaten oder kommerziellen Nutzer empfangen werden kann. Zugleich kam es in den letzten drei Jahren zu einem Preisverfall für mobile Handyempfänger, so daß die mit leistungsfähiger Software ausgestattete, bereits DGPS-fähige Kleinstgeräte deutlich unter 500.- DM zu haben sind und so für jede denkbare geowissenschaftliche Anwendung zur Verfügung stehen können (Abb. 1.2.4).
Heute dienen den Nutzern mindestens 26 (+ 8 Reserve) GPS-Satelliten weltweit zur Positionsbestimmung und dies 24 Stunden täglich. Die GPS-Technik hat nicht nur die globale Positionsbestimmung ermöglicht, sondern auch in seiner erweiterten Form des DGPS (Differentielles GPS) das globale Vermessungswesen revolutioniert. Mit der Schaffung eines World Geodetic Systems 1984 (WGS 84) läßt sich nun mit dem GPS an fast jedem Ort der Welt die Position (bezogen auf WGS-84) bestimmen und in lokale Bezugssysteme umrechnen (s.u.). Vermutlich wird die GPS-Technlogie in zehn Jahren so alltäglich sein, wie es heute Funktelefone sind.

Abb. 1.2.4: Modernes Hand-GPS 60 mit integrierter Navigationssoftware der Firma GARMIN (GARMIN, 2005)
Warum WGS-84?
Die Beschreibung der Satellitenbewegung, die Modellierung der Beobachtungsgrößen und die Darstellung sowie Interpretation der Ergebnisse der Positionsbestimmung muß in geeigneten, wohldefinierten und reproduzierbaren Bezugssystemen erfolgen (Seeber, 1989). Bezugsysteme der genauen Satellitengeodäsie sind von Natur aus global und geozentrisch, da die Satellitenbewegung um den Massenmittelpunkt der Erde erfolgt (vgl. auch Abb. 1.1.4 ). Terrestrische Messungen haben von Natur aus nur lokalen Charakter und werden in der Regel in lokalen Bezugssystemen ausgedrückt. Diese sog. partikularen Systeme sind nicht identisch (!!), so daß die Bereitstellung genauer Transformationsbeziehungen zwischen den Systemen und den Satellitendaten notwendig wird.
In der Satellitengeodäsie werden deshalb zwei Bezugssysteme benötigt: Ein raumfestes, inertiales Bezugssystem (Conventional Inertial System = CIS) zur Beschreibung der Satellitenbahnen und ein erdfestes, terrestrisches Bezugssystem (Conventional Terrestrial System = CTS) zur Festlegung der Beobachtungspunkte und der Ergebnisse der Messung auf der Erdoberfläche (Abb. 1.2.5).
Eine gute Annäherung an ein CIS stellt das Äquatorsystem der sphärischen Astronomie dar, welches durch einen Katalog von Positionen einiger Fundamentalsterne und kosmischer Konstanten in Bezug zum Massenschwerpunkt des Gesamtsystems (meist Erdmassenpunkt) definiert wird. Ein geeignetes erdfestes Bezugsystem muß mit der Erde verbunden sein und wird z.B. historisch durch den Nullmeridian von Greenwich in Verhältnis zum Äquator und den Rotationspolen der Erde definiert (vgl. Kap. 1.1).
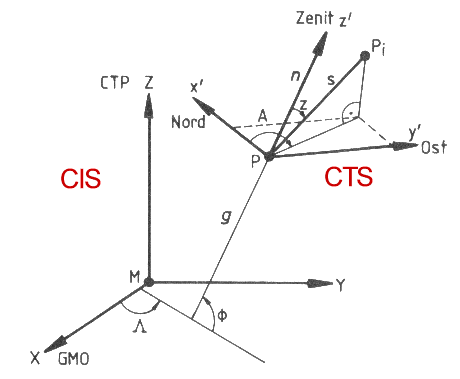
Abb. 1.2.5: Beziehung der Raumkoordinaten von CTS und CIS (Seeber, 1989)
Das World Geodetic System von 1984 (WGS-84) stellt ein in der praktischen Anwendung bewertes ellipsoides CTS dar, welches versucht die tatsächliche Erdfigur bestmöglich in Form eines Rotationsellipsoiden mathematisch global zu beschreiben. Die Erde stellt annähernd einen solchen geometrischen Körper dar, weil sie durch die Rotation an den Polen abgeplattet ist (beitseitig ca. 21 km) und somit eine Meridianellipse um ihre kleine Achse formt. Diesem globalen ellipsoiden System kann mit den ellipsoiden Größen Breite, Länge und Höhe ein kartesisches Koordinatensystem (Rechtssystem) mit den Koordinaten X, Y und Z zur Seite gestellt werden, dessen Koordinaten wiederum in ein lokales System überführt werden können (Abb. 1.2.6).
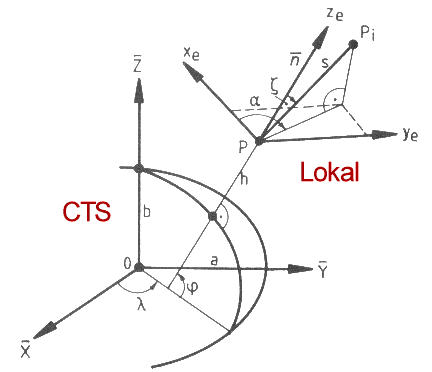
Abb. 1.2.6: Beziehung der Raumkoordinaten des ellipsoiden CTS (z.B. WGS-84) und einem lokalen Bezugssystem (Seeber, 1989)
Berechnungen auf dem Ellipsoid sowie die Einführung geeigneter ebener Koordinatensysteme (z.B. WGS-84, UTM oder Gauss-Krüger) werden über Gebrauchsformeln zur Koordinatentransformation durchgeführt. Prinzipiell müssen die Verschiebungsparameter, die Achsenrotation und der Maßstabsfaktor für eine Datumstransformation aller drei Dimensionen bekannt sein. Für das Geodätische Weltsystem 1984 sind darüber hinaus die Parameter des Erdschwerefeldes und Fundamentalkonstanten wie Lichgeschwindigkeit, Rotation oder geozentrische Gravitationskonstante notwendig. Es besitzt somit ein globales Datum und ist deshalb für die GPS-Messung besonders geeignet.
Die Modellfigur eines Rotationsellipsoiden ist der realen physischen Erdoberfläche nur im Mittel angepaßt. Es handelt sich also um eine mathematisch angenäherte glatte Fläche, auf der mathematische Operationen einfacher auszuführen sind. Das Ellipsoid hat sich deshalb als Bezugsfläche für Lagekoordinaten durchgesetzt und bewährt. Als Höhenbezugsfläche ist das Ellipsoid weniger geeignet. Hier wird allgemein das Geoid als Niveaufläche des Erdschwerefeldes verwendet, da es dem Ozeanspiegel bestmöglich angepaßt ist und sich theoretisch unter den Kontinenten fortsetzt (Abb. 1.2.7).
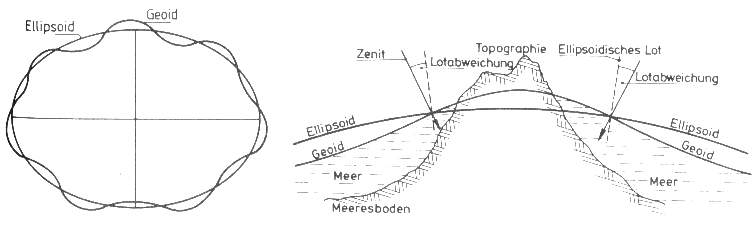
Abb. 1.2.7: Beziehung zwischen Geoid und Ellipsoid (Seeber, 1989)
Die Abweichung des Geoids vom gewählten Referenzellipsoid heißen Geoundulationen N. Diese können für ein globales Referenzellipsoid bis zu 100 m betragen. Zwischen nivellierter, orthometrischer Höhe H (üNN) , ellipsoidischer Höhe h und Geoidundulation N besteht näherungsweise die Beziehung (nach Seeber, 1989):
h = N + H
Es wird deutlich, daß für die gemeinsame Behandlung von dreidimensionalen Positionen der Satellitengeodäsie und ihrer Transformation in terrestrische Positionen die Kenntnis der lokalen Geoidundulation notwendig ist. Zusätzlich gibt es neben den globalen Referenzellipsoiden, von dem sich z.B. das WGS-84 ableitet auch lokal berechnete, bestanschließende Ellipsoide, welche sich auf nur eine bestimmte Region beziehen und so die Grundlage lokaler Landesvermessungssysteme darstellen. Die Beziehung zwischen einem solchen lokalen Ellipsoid und dem globalen geodätischen Bezugssystem heißt Geodätisches Datum (z.B. für Gauss-Krüger mit Rechts - und Hochwerte ist dies Potsdam Bezug auf das Bessel-Ellipsoid!).
