3.7 Klassifikationen
Hintergrund
Bei der Interpretation und Analyse von digitalen Fernerkundungsdaten geht es grundsätzlich darum, raumbezogenen Informationen zu gewinnen, welche später in thematische Kartenwerke überführt oder mit anderen punktuell gewonnenen Geodaten verknüpft werden (vgl. Kap. 4) . Neben der visuellen Interpretation von digitalen Bildern können multispektrale Aufnahmen auch zielgerichtet und automatisiert hinsichtlich der Verteilung von definierten Geo-Objektklassen und deren Pixelwerte untersucht werden. Eine Objektklasse stellt eine vom Interpreten definierte Gruppe von Geo-Objekten dar, welche für die Zielsetzung der Analyse relevant ist (z.B. Nadelwälder, Laubwälder, Ackerflächen, Bebauung, Gesteinstypen, Bodenarten, etc.).
Im Idealfall (!) ist jede Objektklasse durch eine ihr typische multispektrale Signatur im digitalen Bild gekennzeichnet. Diese Multispektralsignatur wird durch die statistische DN-Verteilung der Pixel einer jeden Klasse hervorgerufen, so daß man versuchen kann, mit Hilfe mathematischer Algorithmen die Pixel eines multispektralen Bildes im Hinblick auf ihre Homogenität sowie räumliche Verteilung (und damit die Verteilung von Objektklassen) zu untersuchen.
Die mathematisch-statistische Analyse wird mit Hilfe von Klassifikatoren unüberwacht, selbständig (unsupervised) oder überwacht, interaktiv (supervised) am Rechner über alle verfügbaren Kanäle (Merkmalsraum) sowie deren Derivate (z.B. Ratios) durchgeführt; man spricht deshalb auch einer multispektralen Klassifikation digitaler Fernerkundungsdaten. Die Güte einer Klassifikation hängt dabei wesentlich davon ab, wie eindeutig die Multispektralsignatur jeder Objektklasse ist, wie stark die stichprobenhafte Geländekenntnis (ground truth) in einem Testgebiet mit den Ergebnissen der Klassifikation harmonisiert und mit welchem Typ von Klassifikatoren gearbeitet wird.
Im Regelfall führen unüberwachte Klassifikationen von multispektralen Fernerkundungsdaten zu keinen befriedigenden Gesamtergebnissen, da kaum jede Objektklasse eindeutig im Bild gekennzeichnet ist (es resultieren häufig Mischpixel = Mixel = Fehlklassifikationen!). Deshalb setzt man überwiegend auf überwachte, interaktive Klassifikationsschritte, welche maßgeblich von den Interpreten gesteuert werden können und, gestützt durch individuelle Sach- bzw. Geländekenntnisse, deutlich bessere Klassifikationsergebnisse erbringen.
Pixel- oder Spektralsignaturen oben
Jedes Pixel einer Objektklasse ist in einer dreikanaligen Falschfarbenkomposite statistisch durch seine Lage innerhalb des dreidimensionalen Merkmalsraumes (feature space) charakterisiert. Je unabhängiger bzw. eindeutiger die Lage einer Pixel-Gruppe/-wolke (pixel cloud) einer Objektklasse zugeordnet werden kann, desto besser sind die Klassifikationsmöglichkeiten! Aufgabe der Bearbeiter im Vorfeld einer Klassifikation multispektraler Daten ist es nun, möglichst dekorrelierte Datensätze und eindeutige Trainingsgebiete zu definieren, in denen die jeweilige Objektklasse durch ihre typische Pixelsignaturen statistisch charakterisierbar sind.
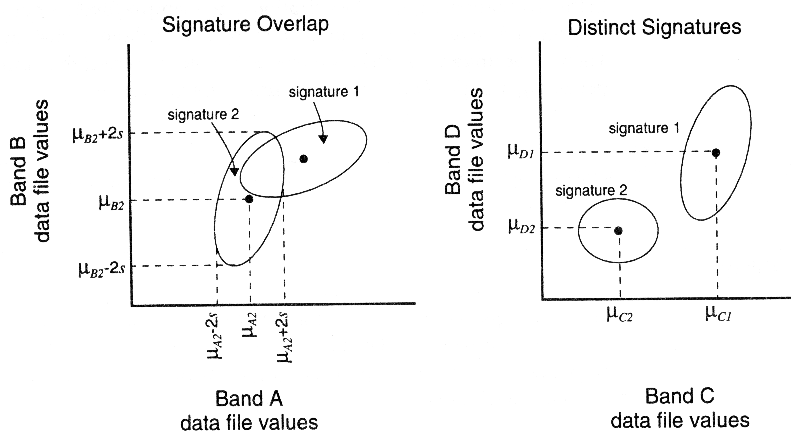
Zur Veranschaulichung dieses Zusammenhanges soll im folgenden von einem zweidimensionalen Merkmalsraum (entsprechend zweier Kanäle) ausgegangen werden. Die Grauwerte einer bestimmten Objektklasse (z.B. Vegetation) unterscheiden sich fortlaufend von Kanal zu Kanal, obwohl es gewisse Ähnlichkeiten der DN-Werte in bestimmten Bandbreiten zu geben scheint (z.B. hohe Korrelationen innerhalb des VIS oder innerhalb des IR). Demzufolge unterscheiden sich auch die Pixelwolken in ihrer Eindeutigkeit, je nach Definition des Merkmalsraumes durch die jeweiligen Kanäle (Abb. 3.7.1).
|
Abb. 3.7.1: Lage zweier |
Es wird deutlich, daß nur Kanalkombinationen für Klassifikationen günstig sind, die hinsichtlich der zu differenzierenden Objektklassen so wenig Mischpixel (Mixel) wie möglich aufweisen. Je größer die Schnittmenge im Merkmalsraum, desto uneindeutiger die Klassenzuweisung von Pixelgruppen! Dieser Sachzusammenhang stellt hinsichtlich der Klassifikationsbemühungen mehrerer Geo-Objektklassen auf der Basis nur eines multispektralen Bildes die Haupschwierigkeit dar, denn fast jede Objektklasse weist in den Originalkanälen neben uneinheitlichen interne Spektralsignaturen auch einen hohen Grad der Mixel-Bildung auf. Oft wird deshalb versucht, die einzelne Spektralsignatur durch den OIF, die Ratiobildung, eine HKA o.ä. deutlicher statistisch herauszuarbeiten, so daß die Eindeutigkeit der einzelnen Signaturen verbessert werden.
Cluster-Analyse (unüberwachtes Klassifizierungsverfahren) oben
Das einfachste unüberwachte Klassifizierungsverfahren stellt die Cluster-Analyse dar, welche die Gesamtheit der Bildelemente in eine Anzahl von Klassen ähnlicher spektraler Eigenschaften unterteilt. Dabei handelt es sich um rein statistische Klassen; ein Bezug zu Geo-Objekten ist a priori nicht gegeben - somit werden auch keine Trainingsgebiete oder andere Referenzdaten gebraucht (Albertz, 1991) .
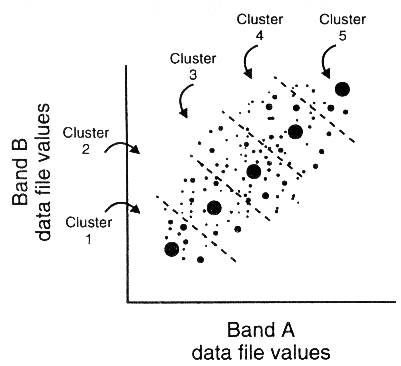
Prinzipiell wird bei diesem Verfahren jedes einzelne Pixel auf seine spektrale Distanz zu einem Mittelwert einer zuvor über die statistischen Gesamtparameter definierten Gruppe von Klassen untersucht, wobei das Pixel jener Klasse zugeschlagen wird, zu der die geringste Distanz (Abweichung) besteht (Abb. 3.7.2). Die Bedeutung der Klassen ließe sich dann nachträglich (posteriori) auf ihre geowissenschaftliche Relevanz untersuchen. Meist führt diese Methode im Detail zu nur unzureichenden Ergebnissen; allerdings wird die Cluster-Analyse im Vorfeld der überwachten Klassifizierung als Beurteilungskriterium für die spektrale Homogenität der ausgewählten Trainingsgebiete bzgl. der Objektklasse oder evtl. möglicher Unterklassen genutzt, da sie nicht sehr rechnenaufwendig ist.
|
Abb. 3.7.2: Schematische Definition von Pixel-Clustern (Objektklassen) und ihren Mittelwerten (ERDAS, |
Minimum-Distance-Verfahren (überwachtes Klassifizierungsverfahren) oben
Bei den überwachten (supervised) Klassifikationen ist das Verfahren der 'Nächsten Nachbarschaft' (Minimum-Distance- oder auch Nearest-Neighbour-Klassifikation) die einfachste Methode rasch relativ akzeptable Klassifikationsergebnisse zu erlangen.
Dabei werden zunächst für die Trainingsgebiete jeder Objektklasse die Mittelwerte der einzelnen Spektralkanäle berechnet (Abb. 3.7.3). Für jedes zu klassifizierende Bildelement berechnet man anschließend den Abstand zu den Mittelpunkten aller Klassen; das Pixel wird dann jener Klasse zugeteilt, zu deren Mittelpunkt der Abstand am geringsten ist (Richards, 1993; Haberäcker, 1987). Oft kommt es aber zu Fehlklassifikationen von Pixeln, da die spektrale Streuung innerhalb einer definierten Klasse im ausgewählten Testgebiet erfahrungsgemäß hoch ist. Da die Klassifikation jedoch überwacht durchgeführt wird, kann nun interaktiv die Wahl des Trainingsgebietes oder die Änderung der Bandkombination eine Verbesserung in der Klassifikation erbringen. Grundsätzlich werden immer alle Pixel irgend einer Klasse zugeordnet.
Abb. 3.7.3: Schematische Definition von Pixel-Klassen mit ihren Mittelwerten und der Zuweisung von Testpixeln (1,2,3) aufgrund der bestehenden spektralen Distanz (Albertz, 1991) |
Parallelepiped-Verfahren (überwachtes Klassifizierungsverfahren) oben
Unter den überwachten (supervised) Klassifikationen ist das Verfahren der Parallelepiped-Bildung (oder auch 'Quader-' bzw. 'Box'-Klassifikator) eine einfache, aber bereits rechenaufwendigere Methode.
Dabei werden zunächst für die Trainingsgebiete jeder Objektklasse die obere und untere Spektralgrenze (meist +/- 2 x Standardabweichung) über die interaktive Auswahl der Trainingsgebiete definiert (im zweidimensionalen Raum also Rechtecke bzw. 3D als Quader). Alle Pixel werden nun entsprechend der Eckdaten der ausgewählten Objektklassen auf ihre mögliche Zugehörigkeit zu den verschiedenen Parallelepipeden geprüft. Pixel, welche in keine Klasse fallen bleiben unklassifiziert. Bei hoher Mixelrate müssen die einzelnen Quader in viele kleinere 'Boxen' zerlegt werden, damit die Pixelhaufen besser aufgelöst werden können (Abb. 3.7.4). Hier können Pixel auch unklassifiziert bleiben.
Abb. 3.7.4: Schematische Definition von Pixel-Klassen über untere bzw. obere Grenzwerten und den aus ihnen abgeleiteten Quadern. Bei starker Mixelbildung werden die Klassen durch eine Kombination kleinerer Parallelepipede definiert (Albertz, 1991) |
Maximum-Likelihood-Verfahren (überwachtes Klassifizierungsverfahren) oben
Unter den überwachten (supervised) Klassifikationen ist das Verfahren der 'Größten Wahrscheinlichkeit' (oder auch Maximum-Likelihood) eine sehr genaue aber auch aufwendige Methode Pixel zu klassifizieren.
Der Klassifikator berechnet aufgrund statistischer Kennwerte der interaktiv ausgewählten Trainingsgebiete (Pixelgruppen) die Wahrscheinlichkeiten, mit denen einzelne Pixel den Klassen angehören könnten. Dabei unterstellt man, daß die Pixelgruppen jeder Objektklasse im Merkmalsraum eine Normalverteilung um den jeweiligen Klassenmittelpunkt aufweisen. Zunächst werden so alle Pixel verschiedenen Klassen zugeordnet (mit Wahrscheinlichkeiten von [P] zwischen 100% u. 0%). Bei starker Korrelation innerhalb der Kanäle kommt es in einem zweiten Schritt dann zur Bildung von individuell definierten Ellipsoiden mit Ebenen gleicher Wahrscheinlichkeit (Rückweisungsschranken) für jede Klasse (Abb. 3.7.5), sogenannte Mahalanobis-Ellipsoide: Erst hier können Pixel auch unklassifiziert bleiben, sofern sie die 'Mindestwahrscheinlichkeit' nicht erreichen.
Abb. 3.7.5: Schematische Definition von Pixel-Klassen über Ellipsoide gleicher Wahrscheinlichkeit - hier P von 60% und 70% (modifiziert nach Albertz, 1991) |
Hierachische Klassifikation (überwachtes Klassifizierungsverfahren) oben
Unter allen Klassifikationsverfahren nimmt die Hierachische bzw. Verzweigungsklassifikation eine Sonderrolle ein, da sie sich grundlegend von den obigen Verfahren unterscheidet. Die Zuordnung von Pixeln in Klassen erfolgt nicht über einen einmaligen Vorgang, vielmehr wird das endgültige Erbegnis über eine Folge von Itterationen erreicht.
Dabei wird zunächst nur zwischen zwei bis drei Klassen unterschieden, welche dann wiederum in Einzelklassen zerlegt werden (Abb. 3.7.6). Dieses Verfahren ist generell sehr flexibel und für viele Klassifikationsansätze zu gebrauchen; allerdings erfordert die Aufschlüsselung in viele Klassenebenen ein hohes Maß an Systematik und Übersicht! Ein großer Vorteil dieses Klassifikationsansatzes liegt auch in der zielgerichteten Kanal- bzw. Komponentenauswahl für jeden einzelnen Zuweisungsschritt. So lassen sich unabhängig für jede Klassifikation Originalkanäle, Hauptkomponenten, Ratios etc. individuell auswählen. Der interaktive Arbeitsaufwand ist jedoch insgesamt deutlich höher, als bei den oben angesprochenen Verfahren.
Abb. 3.7.6: Schematischer Ablauf einer hierachischen Klassifizierung über einen Entscheidungsbaum (Albertz, 1991) |
Güte von pixelbasierten Klassifikationsergebnissen oben
In der Praxis ist die Anwendung der Multispektral-Klassifizierung oft schwieriger, als man zunächst annimmt. Tatsächlich sind die mathematischen und geowissenschaftlichen Grundannahmen der Methoden nur annähernd erfüllt bzw. starken Schwankungen unterworfen. Insbesondere stellen wir immer wieder fest, daß die theoretisch erhoffte reine Spektralsignatur für eine Objektklasse nicht gegeben ist; d.h. die in den Trainingsgebieten abgegriffenen repräsentativen Pixelgruppen zeigen im Merkmalsraum starke Überlappungen (z.B. Vegetationsarten bzw. -zustände). Die Gründe liegen in dem hohen Mixelanteil innerhalb der einzelnen Klassen, da bei einer geometrischen Auflösung von z.B. 30m/Pixel (bei TM) ein Gesamtreflexionswert über eine 900qm große Fläche aufgenommen wird!
Zudem sind Inhomogenitäten in der Ausbildung einzelner Objektklassen der Regelfall: Weizenfelder sind unterschiedlich reif oder exponiert, Siedlungsräume individuell gestaltet, Wald- oder Moorflächen je nach Standort unterschiedlich entwickelt, Böden oder Gesteine unterschiedlich durchfeuchtet usw..
Ein wesentlicher Faktor der Mixel-Bildung ist auch der unterschiedliche Beleuchtungswinkel (morphologische Exposition der Objektklasse zum Sensor, also das Geländerelief!). So beinflussen Schattenwurf, wechselnde Reflexionsarten (total oder diffus) den resultierenden DN-Wert, obwohl keine materialspezifischen Variationen innerhalb der Objektklasse vorliegen.
|
Abb. 3.7.7: Maximum- |
Insgesamt unterliegt die Multispektral-Klassifizierung einer Vielzahl von störenden Einflüssen. Aus diesem Grunde verlangt die Anwendung der Methoden Sorgfalt, Sachkenntnis und viel Erfahrung! Bei der Interpretation und kartograpischen Umsetzung der Ergebnisse müssen die methodischen Grenzen des Verfahrens stets bedacht und einzelne Klassen individuell auf Basis unterschiedlicher Bildkomponenten erarbeitet werden!
Erweiterte Klassifikationsstrategien oben
Weiterführende Klassifikationsansätze (z.B. objekt-orientiert) steigern die Güte einer Klassifikation durch den vermehrten Einsatz zusätzlicher Daten in Form 'künstlicher Kanäle' (Abb. 3.7.8) . Dabei fließen Informationen wie weitere Fernerkundungsdaten (z.B. Luftbilder), Geologie, DGM, Bodentyp, Niederschläge, Geometrie, Textur etc. in die Klassifizierung mit ein - der Merkmalsraum wird also signifikant erweitert.
Abb. 3.7.8: Zusatzdaten einer multispektralen Klassifikation in Form 'künstlicher Kanäle' (Albertz, 1991) |
Von zunehmender Bedeutung sind vor allem auch Texturparameter, welche über Algorithmen in die Klassifikation miteinbezogen werden. Dabei wird die Textur als typisches Muster einer Objektklasse definiert und können über Parameter wie Lebhaftigkeit, Stärke, Ausrichtung, Intensität u.ä. beschrieben sein (Rengers & Prinz, 2009).
Auch spielt die multitemporale Betrachtung von Datensätzen (d.h. zu unterschiedlichen Zeitpunkten) ein wesentliche Rolle für die Ergebnisse einer Klassifikation. Werden hier starke zeitabhängige Variationen festgestellt, kann auch von einem Monitoring einer bestimmten Region gesprochen werden.
Klassifikationsablauf unter ERDAS Imagine (Praktikum) oben
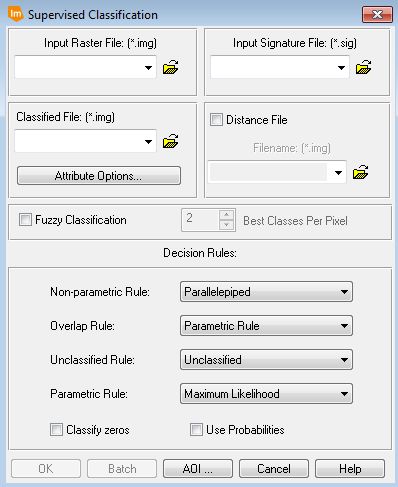
In der Praxis ist die Anwendung der Multispektral-Klassifizierung oft sehr schwierig, da man auf eine kaum zu überschaubare Vielfalt von statistischen Entscheidungshilfen/-kriterien bei der Zuweisung von Pixeln in Klassen stößt. ERDAS Imagine bietet hier einen strukturierten Verlaufpfad für die Zuweisung von Pixeln an, wobei einerseits die Pixel-Statistisk innerhalb eines Trainingsgebietes als Zuweisungskriterium gewählt wird (engl. parametric rule), oder unabhängig vom Trainingsgebiet eine Zuweisung über die Pixel-Wolke (scattergramme, feature space..) stattfindet (non-parametric rule). Hierbei entscheidet der Bearbeiter, ob ein ursprünglich unklassifiziertes Pixel unklassifziert bleibt oder rückwirkend einer Klasse zugewiesen wird (Abb. 3.7.9a und b).
Abb. 3.7.9a: Zuweisung eines Pixels in Klassen unter ERDAS Imagine (ERDAS, 1997) |
|
Abb. 3.7.9b: Klassifikation nach ausgewählten Trainingsgebieten unter ERDAS Imagine (ERDAS, 2015) |
Objektorientiertes Klassifizieren (OBIA) oben
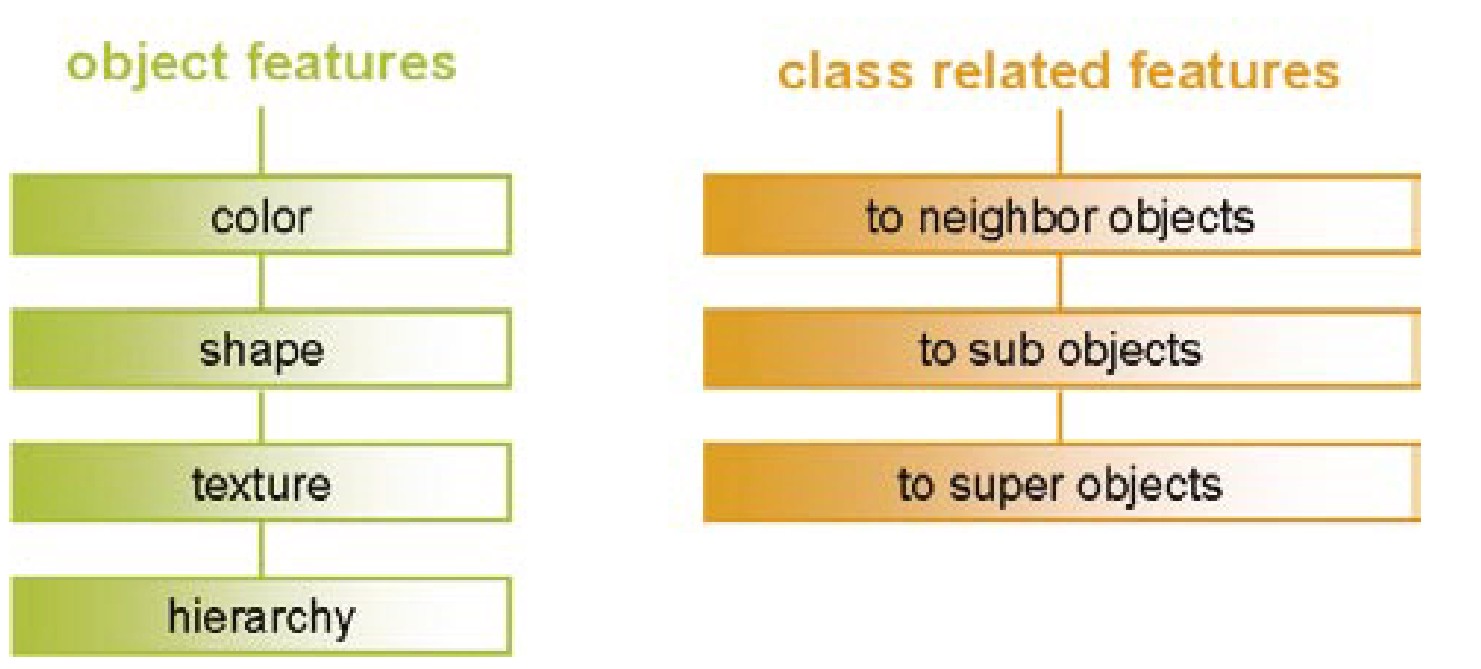
Im Gegensatz zu einer rein spektralorientierten, pixelorientierten Klassifikation versuchen objektorientierte Klassifikationsmethoden (wie z.B. innerhalb des Programmes eCognition) Segmentobjekte durch itterative Segmentation über Parameter (Abb. 3.7.10) wie
- Farbton (i.A. DN-Wert)
- Texturen
- Topologie/Kontex
- Zusatzinformation anderer Ebenen
- etc...
vordefinierten Klassen (oder auch Subklassen) zuzuordnen um so 'Objekte' zu charakterisieren (Object Based Image Analysis = OBIA) .
Grundlegend ist die Definition von Testobjekten (sog. sample objects, hier: Pixel oder Pixelgruppen!), welche zu einem hierachischen Verbund von Objektklassen zusammengeführt werden. Im gesamten Bild werden diese auf der Basis einer zuvor vorgenommenen Segmentierung abgegrenzt und statistisch verglichen. Ist ein Objekt erfolgreich klassifiziert, vererbt es seine Charakteristika (z.B. den Zuweisungsschlüssel) mittels Fuzzy-Logic oder Zusatzinformationen anderen Segmenten.
|
Abb. 3.7.10: Parameter objektorientierter Klassifikation (eCognition, 2003) |
Basis der multivarianten Segmentation ist die Verfügbarkeit unterschiedlicher Informationsebenen (Layer), welche nicht nur aus FE-Daten, sondern auch aus anderen GIS-Graphikdaten bestehen können. Im gemeinsamen Datenpool werden kleinste gemeinsame Nenner gesucht, die dann schrittweise ein Flächenwachstum erfahren um Objekte zu bilden. Das Verschneiden (merge) von vielen kleineren Objekten zu einem großen Objekt gleicher Signatur wird schrittweise geprüft und realisiert (Abb. 3.7.11). In der Regel geht man von einen nur einem Pixel großen Nucleus aus, dessen Eigenschaften über Grauwertstatistik, Homogenität und Form im Wachstum kontrolliert werden (z.B. mittels heuristischer Optimierung).
|
Abb. 3.7.11: Segmentiertes Wachstum von Objekten (eCognition, 2003) |
Die eigentliche Klassifikation kann in zwei unterschiedlichen Varianten erfolgen (Abb. 3.7.12):
I. Testklassen werden direkt über Pixelzuordnung bestimmt (sample based). Diese Methode ist einfach und erlaubt eine rasche interaktive Selektion von Objekten bzw. deren Interpolation über das ganze Bild
II. Alle Objekte werden auf einer heterogenen Wissenbasis (knowledge base) definiert und im gesamten Bild mittels Vergleich von Eigenschaften sowie deren Vererbung miteinander verglichen und zu einer klassenspezifischen Kontextinformation verknüpft (class related features). Dies ist ein aufwendiges Verfahren mit jedoch guten Ergebnisse.
|
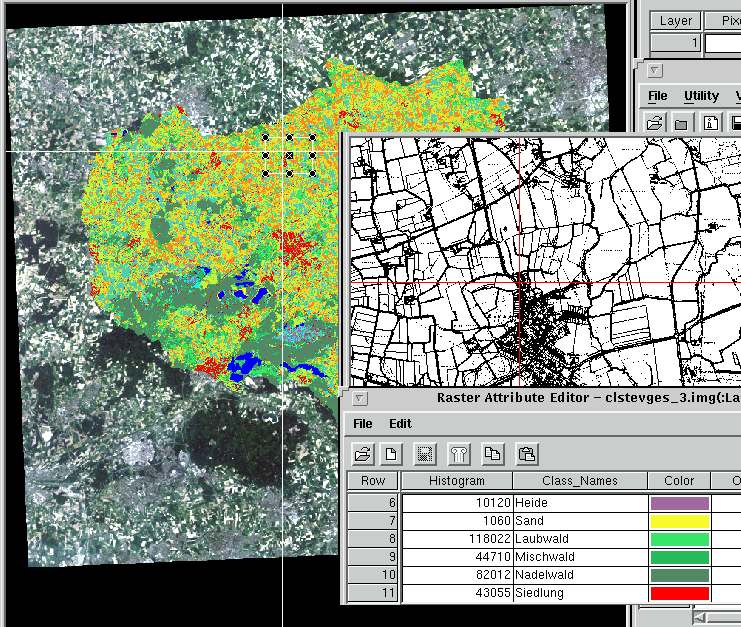
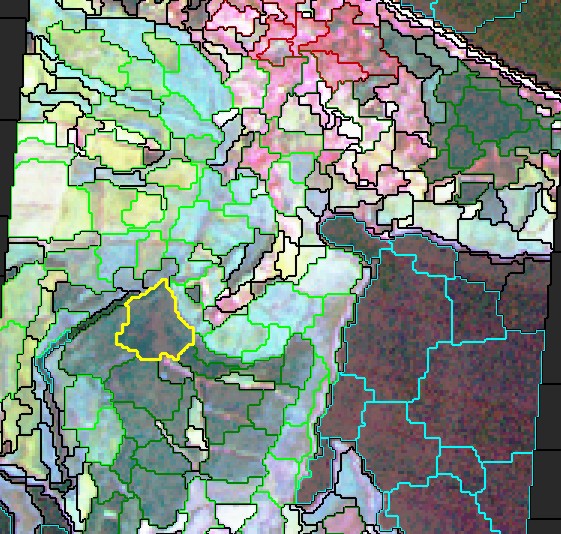
Abb. 3.7.12: Grundlegende Segmentierung (zu Objekten) eines multispektralen Landsat TM Bildes von Zinnowitz/Usedom in eCognition. Das ausgewählte gelbe Objekt stellt ein Testgebiet für die Klasse Wald dar. |
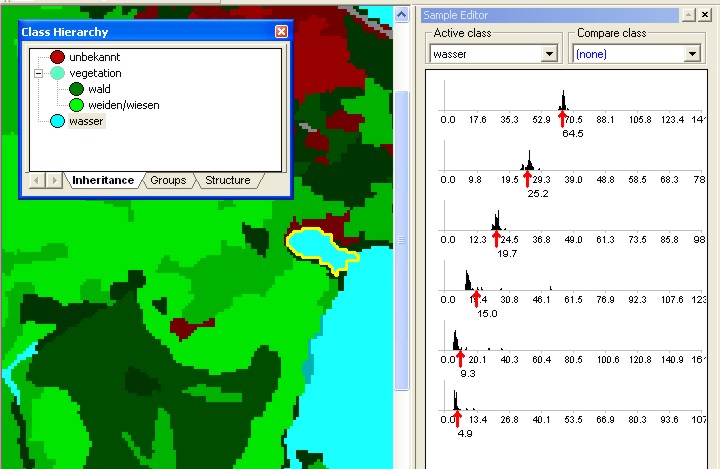
Die eigentliche 'sample based' Klassifikation erfolgt dann über die weitere Zuweisung von Objekten zu Klassen und deren Vergleich mit benachbarten Objekten hinsichtlich ihrer statischtischen Merkmale. Es resultieren Klassifikationen, die itterativ verbessert, d.h. um einzelne Segmente erweitert oder zu Hierachien modifiziert werden. Dabei ist die statistische Lage der Segmente (Klassenobjekte) im Merkmalsraum einer Klasse direkt einsehbar (Abb. 3.7.13).
|
Abb. 3.7.13: Klassifi- |
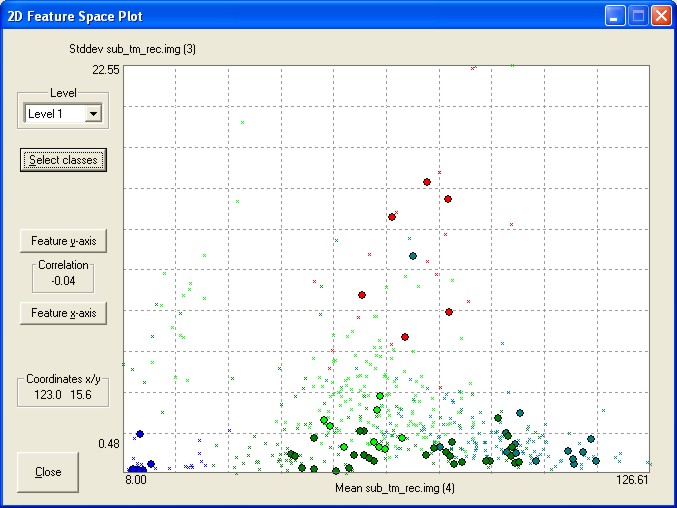
Eine Optimierung der Testgebiete (sample objects) kann in der Regel einfach über den multivarianten Merkmalsraum erfolgen (Abb. 3.7.14). Hier werden die Klassen in ihrer relativen Lage gegenüber benachbarten Klassen abgebildet und erleichtern so das direkte Schätzen einer Signifikanz jedes repräsenativen Testgebietes für die jeweilige Klasse. Je weiter der Abstand der Objekte voneinander, desto weniger Unsicherheit ist in der späteren Klassifikation gegeben.
|
Abb. 3.7.14: Verschiedene Klassen im zwei-dimensionalen Merkmalsraum. Die Testgebiete zeigen im gemeinsamen Scattergram sichbares Rot zu nahem IR des TM Scanners deutliche Signifikanzen (z.B. rote und blaue Klassen/Testgebiete). Innerhalb der Vegetationsklassen (grün) kommt es jedoch zu Über-schneidungen. |
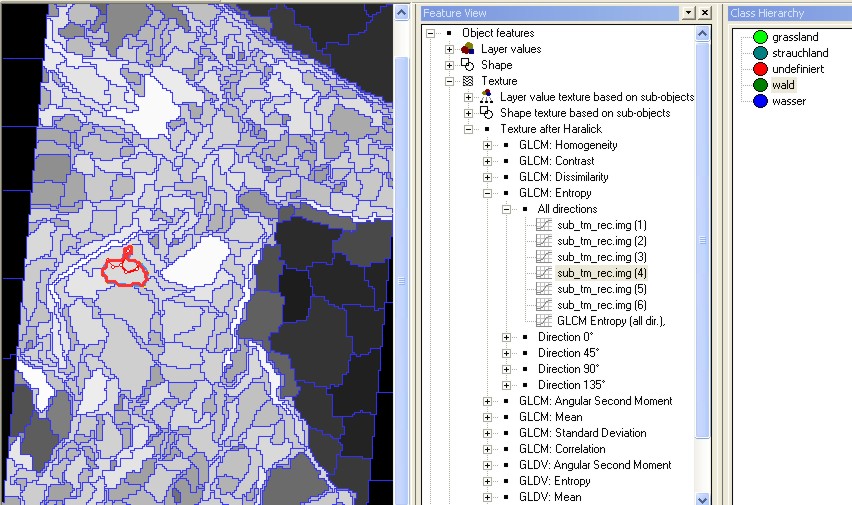
Eine weiter Optimierung der Testgebiete (sample objects) erfolgt über die Einbindung und Berücksichtigung der heterogenen Wissensbasis. So kann z.B. die Textur, Topologie, Form etc. eines jeden Testgebietes als weitere Charakteristik hinzugezogen werden und in der erneuten Klassifikation Berücksichtigung finden (Abb. 3.7.15). Die Authentizität der einbezogenen Charakteristika ist in Form der neuen Polygonbildung für jede Klasse direkt sichtbar.
|
Abb. 3.7.15: Polygonale Abschätzung der Authentizität des zusätzlichen Charakteristikums Textur für den Kanla 4 des TM Scanners im Bild Zinnowitz/ Usedom. Die Grauwert-verteilung ist hier das Maß der Repräsentanz hinsichtlich Klasse und Polygon. |
Am Ende der multivarianten, objektorientierten Klassifikation steht also eine Zusammenstellung von Klassen, deren Charakteristika aus einer Vielzahl (idealerweise) einzigartiger, repräsentativen Eigenschaften steht.
oben